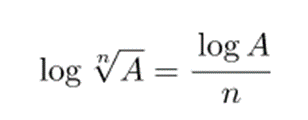En esta página encontrarás qué logaritmo funciones y también cómo representarlas en una gráfica. Además, verás todas sus características, cómo calcular su dominio y varios ejemplos para entenderlo mejor. Finalmente, podrás practicar con ejercicios y problemas resueltos paso a paso de funciones logarítmicas.
La definición de una función logarítmica es la siguiente:
En matemáticas, las funciones logarítmicas son aquellas funciones cuya variable independiente x forma parte del demostración de un logaritmo. Es decir, son de la sucesiva representación:
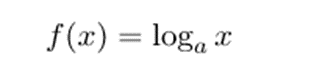
Donde es forzosamente un número real positivo y diferente de 1.
Por ejemplo, la siguiente función es logarítmica:
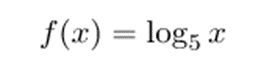
Antes de ver las tipos de las funciones logarítmicas, marchamos a repasar momentáneamente la concepción de logaritmo:
- El logaritmo en base a de y es el mecanismo al que hay elevar el número a para que dé como consecuencia el número y
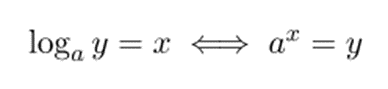
Recuerda asimismo que el logaritmo neperiano (o logaritmo natural) es semejante al logaritmo cuya base es el número exponencial e:
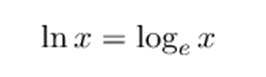
Por otro lado, se suele prescindir la base cuando esta es 10. Este tipo de logaritmos se llaman logaritmos decimales o algoritmos comunes:
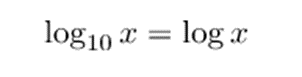
Dominio de una función logarítmica
Un logaritmo solo acepta números positivos, por lo tanto, el dominio de una función logarítmica existirán todos los números que indemnicen esta condición.
A modo de ejemplo, marchamos a calcular el dominio de la sucesiva función logarítmica:
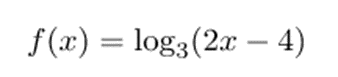
El argumento de un logaritmo tiene que ser más grande que 0, ya que no existen ni los logaritmos de números negativos ni el logaritmo de 0. Así que tenemos que mirar cuándo el argumento de la función es mayor que cero:

De modo que el demostración del logaritmo será más grande que cero si es mayor que 2. Así que el dominio de la función son todos los números más grandes que 2 (no incluido):
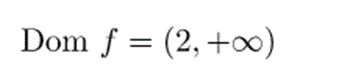
Características de las funciones logarítmicas
- Como tenemos visto, el dominio de una función logarítmica son todas las x que crean que el argumento del logaritmo sea positivo.
- El camino o rango de una función logarítmica son todos los números reales.
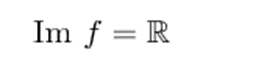
- Toda función logarítmica es una función continua e inyectiva.
- El decrecimiento o crecimiento de una función logarítmica pende de la base del logaritmo: si la base es mayor que 1 (a˃1) a la función es creciente, en cambio, si la base está en del intervalo entre cero y uno (0˂a˂1) la función es decreciente.
- Del mismo modo, la curvatura de cualquier función logarítmica asimismo viene determinada por su base: la función será cóncava si la base es superior a 1, por contra, será convexa si la base es menor que 1.
- La inversa de la función logarítmica es la función exponencial. Por tanto, las gráficas de una función logarítmica y una función exponencial son simétricas respecto de la recta y=x si ambas poseen la misma base.
Cómo constituir una función logarítmica en una gráfica
A continuidad vamos a ver con un ejemplo cómo graficar una función logarítmica.
- Simboliza en un gráfico la siguiente función:
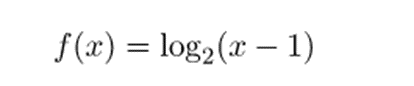
Lo primero que correspondemos hacer es hallar el dominio de la función. Y, como es un logaritmo, su demostración posee que ser más grande que 0, ya que no están ni los logaritmos de números negativos ni el logaritmo de 0. Así que echar un vistazo cuándo el argumento de
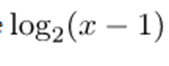
es mayor que 0:
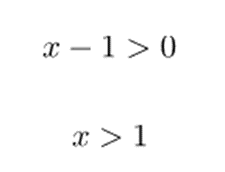
Por tanto, el demostración del logaritmo será positivo si y solo si es mayor que 1. De modo que el dominio de la función son todos los números más grandes que 1 (no incluido):
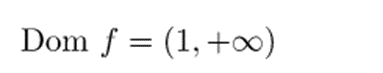
Una vez estar al corriente el dominio de la función logarítmica, opinemos una tabla de valores. Ciertamente, cuantos más puntos se calculen, más exacta será la representación de la función. Pero computando unos 5 puntos dentro del intervalo del dominio es bastante:
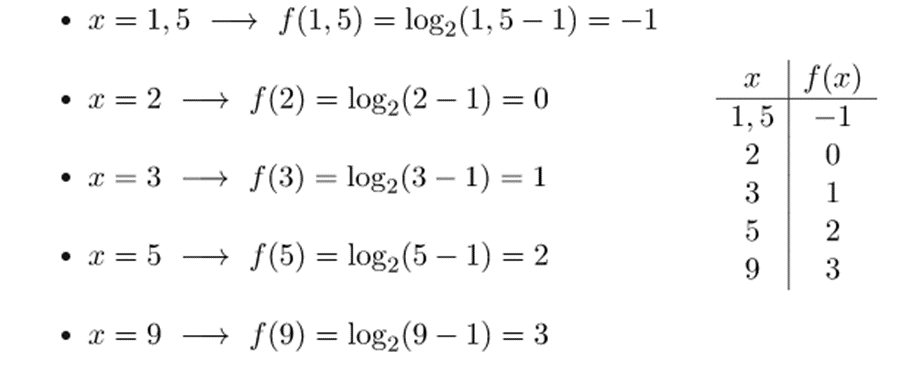
Te encomendamos usar la calculadora para hallar los puntos de la tabla de valores, ya que no son fáciles de calcular a mano. Sin embargo, en cualesquiera calculadoras solo se logran calcular los logaritmos de base 10, en tal caso conmemora que puedes encontrar el resultado de cualquier logaritmo aplicando la propiedad de cambio de base de los logaritmos:
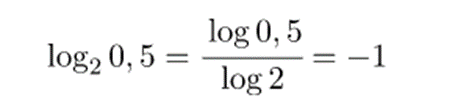
Ahora personificamos los puntos obtenidos en un gráfico:
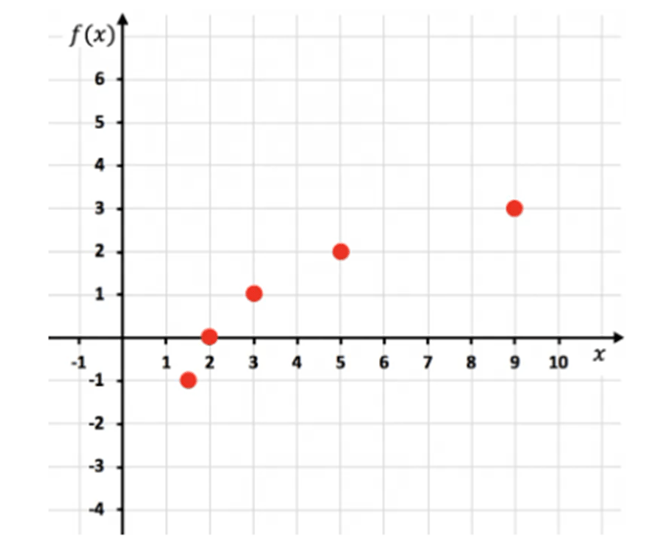
Y posteriormente articulamos los puntos y alargamos la función:
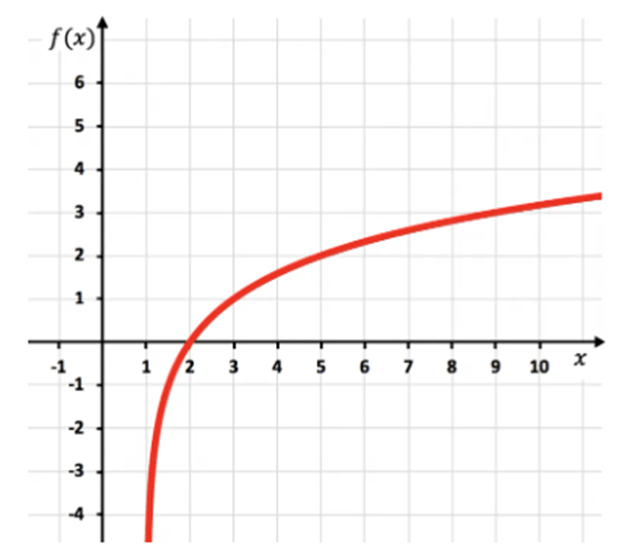
Fíjate que la función por la izquierda sigue decreciendo, en cambio, la función por la derecha va creciendo pero nunca llega a tocar x=1. No obstante se acerca mucho, nunca lo llega a tocar. Eso figura que la recta x=1 es una asíntota vertical de la función.
Propiedades de los logaritmos
A modo de repaso, a continuidad posees las propiedades de los logaritmos por si precisas hacer operaciones con funciones logarítmicas:
- El logaritmo de un producto es semejante a la suma de los logaritmos de los factores.
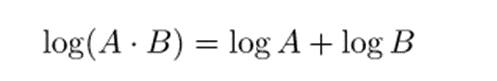
- El logaritmo de un cociente es igual a la diferencia del logaritmo del dividendo – el logaritmo del divisor.
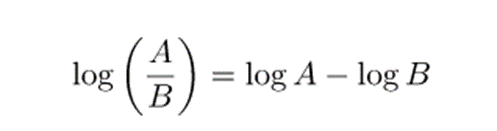
- El logaritmo de una potencia es lo mismo que multiplicar el exponente de la potencia por el logaritmo de la base.
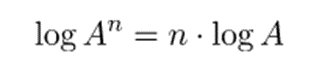
- El logaritmo de una raíz es = a dividir el logaritmo del radicando y el índice de la raíz.