Una fracción es una parte es la expresión matemática que se usa para representar las piezas de un todo. O sea, es un número completo que fue dividido en piezas equivalentes y cada parte es la parte del completo.
Toda parte es una separación y toda separación es una parte. Por esto, una separación se puede transformar en una parte para ser simplificada.
[orbital_cluster categories=»8″ order=»DESC» postperpage=»27″]
Etimológicamente, el concepto parte procede del latín fractio que significa acción de romper.
Ejemplificando, si estamos celebrando un cumpleaños y poseemos 7 invitados, dividimos la pizza o la tarta en 7 piezas equivalentes, o sea, en 7. Cada pedazo corresponde a 1/7 del total y, si el invitado ingiere 3 trozos puede decirse que ha comido 3/7 de la pizza.
Las fracciones se representan por 2 números que permanecen escritos unos sobre otros y separados por una línea divisoria. Esta línea obtiene el nombre de raya fraccionaria.
El número que está encima de la raya fraccionaria es el numerador, que es el número de piezas de la unidad o total. El número que está abajo es el denominador y expresa en cuántas piezas equivalentes se divide la unidad o total.
Ejemplificando, si al final de la pizza o la tarta 3 invitados cogen 3 trozos de los 7 que hay, van a ser (3/7), ya que han cogido 3 piezas equivalentes del total de 7.
¿Cómo se leen las fracciones?
Una vez que leemos fracciones, primero comentamos el numerador, que es el número que sugiere cuántas piezas se permanecen tomando del total. Se lee igual que los números cardinales.
Luego, el denominador puede tener diversos nombres. Ejemplificando, si la unidad se divide en 2 piezas equivalentes, a todas aquellas piezas las vamos a llamar medios; si se separan en 3, tercios; en 4 van a ser cuartos, etcétera. O sea, los denominadores se leen como números partitivos.
Una vez que el denominador es más grande que 10, se incorpora la terminación -avos a partir del número. De esta forma se conforman: onceavos, doceavos, treceavos, y de esta forma en adelante.

Divisibilidad en matemáticas

3 operaciones algebraicas con fracciones

¿Puede resolver estos ejercicios de sumas de fracciones?

3 interesantes ejercicios de suma de fracciones
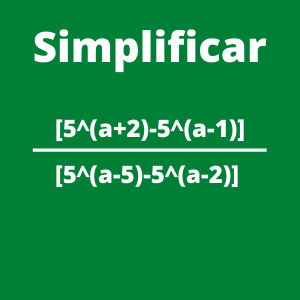
3 ejercicios didácticos para simplificar las fracciones

¿Cómo simplificar una fraccion?
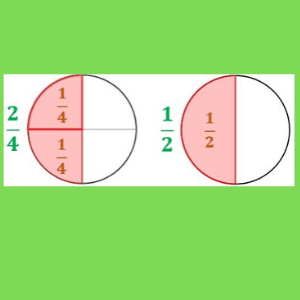
Ejercicios de Fracciones

Resta de fracciones con distinto denominador

4 Sumas de fracciones con diferente denominador

Operaciones con fracciones
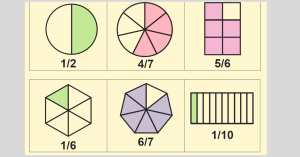
¿Cómo se realiza la suma y resta de fracciones? Ejercicios Resueltos
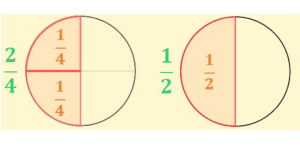
¿Qué es una fracción?
¿Por qué son relevantes las fracciones?
Las fracciones son relevantes ya que nos mencionan el fragmento de un todo. Utilizamos fracciones cada día: para mencionar la hora, dividir las facturas, reservar presupuestos, etc.
Las fracciones las usamos en la vida diaria y es fundamental subrayar su uso en diversos instantes de la vida:
- Una vez que cocinamos y seguimos una receta, hacemos uso de las fracciones. Ejemplo ½ taza de azucar.
- En el momento de ir al mercado requerimos “½ kilogramo de manzanas”
- Al distribuir alimentos entre algunas personas, como en un cumpleaños.
- Al medir la época y expresarlo en fracciones como “en 3/4 empieza la película”.
Tipos de fracciones
Fracciones usuales
Una parte común, además llamada parte fácil es un número racional (aquel que puede representarse como el cociente de 2 números completos o más) donde tanto el numerador como el denominador son números completos.
Fracciones propias e impropias
Las fracciones propias son esas en las que su numerador es menor a su denominador. Ejemplo 6/17.
Las fracciones impropias poseen un numerador igual o más grande que su denominador. Ejemplo 17/6.
Fracciones mixtas
O además llamadas números mixtos, son esas fracciones que constan de una sección completa y otra fraccionaria.
2 5/6
Las fracciones mixtas sirven para redactar unidades de medida (peso, tiempo, capacidad) así como recetas de cocina. Ejemplificando, «una hora y cuarto» se podría representar como 1 1/4.
Fracción inversa
Una parte inversa es una parte en la que se han invertido el numerador y el denominador. Ejemplificando, en 2/3 su parte inversa es 3/2.
Fracción unitaria
En las fracciones inversas, las fracciones unitarias son fracciones habituales que representan a un número racional en la cual el numerador es igual a 1 y el denominador es un completo positivo: 1/2, 1/3, 1/4.
Las fracciones unitarias son los inversos de los números completos positivos. Una vez que más grande sea el denominador, menor va a ser el número racional que representa la parte.
Fracciones iguales
Las fracciones iguales representan la misma porción aun cuando el numerador y el denominador sean diferentes.
Son esas fracciones que tienen la posibilidad de ser simplificadas en otras más pequeñas. Es más simple laborar con fracciones simplificadas ya que nos posibilita equiparar fracciones de forma fácil.
Para eso, se multiplica o divide el numerador y denominador por el mismo número, manteniendo la parte su costo. Ejemplificando ½=2/4=3/6.
Fracción decimal
Es aquella parte que tiene como denominador (el número de abajo) una potencia de 10 como 10; 100; 1 000, etcétera. Los números decimales son en sí un tipo de número fraccionario. Ejemplificando, el decimal 0,5 representa exactamente la parte 5/10 (5 décimas) o 14/100 que podría ser 0,14 (catorce centésimas).
Las fracciones decimales corresponden a las piezas de un número completo que se ha partido en una decena, centena, etcétera., de piezas equivalentes de esta forma, los números con coma decimal permanecen expresando una parte decimal.
¿Cómo solucionar una parte decimal?
- Hallar un número que podamos multiplicar por el denominador para que se convierta en una potencia de 10.
- Multiplicar el numerador
- Redactar el numerador colocando la coma donde corresponde, dependiendo de los ceros del denominador.
Fracción irreducible
Las fracciones irreducibles son divisiones que no se pueden simplificar o minimizar. O sea, el numerador y el denominador no comparten componentes en común, debido a que son primos entre sí. Una vez que una parte es irreducible está escrito en su mínima expresión al no haber otra parte equivalente que se logre redactar de forma fácil.
El numerador y denominador de una parte irreducible no poseen ningún divisor común entre ellos siendo imposible obtener como consecuencia un número completo. Ejemplificando: 2/3, 3/5 y 4/9.
Fracción reducible
A la inversa que las fracciones irreducibles, estas sí tienen la posibilidad de simplificar, debido a que el numerador y el denominador poseen divisores usuales que realizan viable minimizar la parte.
Ejemplificando: en la parte 27/15 el mayor común divisor es 3 y se puede minimizar a 9/5.
Operaciones con fracciones
Sumas y restas con el mismo denominador
Para sumar fracciones con el mismo denominador se suman los numeradores y se preserva el mismo denominador.
2/5+1/5=3/5
Para restar fracciones con el mismo denominador solo se debe restar los numeradores dejando el denominador común.
5/6-2/6=3/6
Sumas y restas de fracciones con diferente denominador
Una vez que las fracciones poseen diferentes denominadores se deben simplificar hasta su más mínima expresión hasta que tengan un denominador común.
Sumas con diferente denominador
La suma de fracciones con distinto denominador se sabe además como fracciones heterogéneas.
Método de la separación de los denominadores por los numeradores
- Ubicar el mínimo común múltiplo de los denominadores que haya
- Multiplicar cada numerador por el número que hayamos multiplicado al denominador
- Sumar los numeradores que se obtienen dejando el mismo numerador
Multiplicación en cruz
- Buscar el común denominador de las fracciones
- Multiplicar los denominadores
- Multiplicar en cruz, o sea, el numerador de la primera parte por el denominador de la segunda parte
- El resultado se sitúa en el numerador con la raya fraccionaria
- Multiplicar el denominador de la primera parte por el numerador de la segunda parte
- El resultado se sitúa en el numerador con la raya fraccionaria
- Suma con los numeradores resultantes
Restas con diferente denominador
Hay algunas maneras de solucionar las restas con diferente denominador, ejemplificando:
- Multiplicar en cruz: Se multiplica el numerador de la primera parte por el denominador de la segunda, y el denominador de la primera por el numerador de la segunda. Las dos multiplicaciones se restan.
- Multiplicar los denominadores de las 2 fracciones y solucionar lo demás de las operaciones hasta minimizar la parte.
¿Cómo multiplicar fracciones?
Para multiplicar fracciones se multiplican “en línea”, o sea, primero se divide el numerador de la primera parte por el numerador de la segunda y después el denominador de la primera parte por el denominador de la segunda.
¿Cómo dividir fracciones?
Para dividir 2 o más fracciones se debe multiplicar en cruz, en otros términos, multiplicando el numerador de la primera parte por el denominador de la segunda parte para lograr el numerador.
Para obtener el denominador, se debe multiplicar el denominador de la primera parte por el numerador de la segunda parte.
Puedes revisar los pasos en el siguiente ejemplo:
(4/5)/(2/1)= (4/5)*(1/2)=4/10=2/5

