El simplificar las fracciones se entiende como disminuir el numerador y denominador a otra fracción con números menores (siendo esta equivalente). Por equivalente entendemos que tiene el mismo valor pero está representado de otra forma.
Para simplificar las fracciones se dividen los números de arriba y de abajo por un mismo valor y nos da como resultado un valor más pequeño pero con números enteros. Ejemplo en vez de decir 6/4 se podría decir 3/2, eso es simplificar. La simplificación es transformar en un equivalente más simple.
Se entiende como la reducción o también llamada simplificación de una fracción al cambio más pequeño que se le realiza sin afectar su valor.
A continuación podemos ver 3 ejercicios didácticos para simplificar las fracciones:
Ejercicio 1 simplificar las fracciones:

Calcula 3^X – 1
Si 7^(X+2)*7^(X-6)=5^0
Partiendo de la ecuación 7^(X+2)*7^(X-6)=5^0 se puede ver que en la parte izquierda, la base es la misma; por lo tanto para su producto se pone la misma base y se suma los exponentes quedando 7^(2X-4)=5^0. Ahora se tiene 5^0 en la parte derecha pero se buscara que todas las bases sean iguales por lo que expresaremos en términos de 7^0 sin modificar el resultado final ya que ambos valores dan 1. Ahora queda la ecuación de la siguiente forma 7^(2X-4)=7^0.
Como las bases son iguales, los exponentes también serán iguales por lo que la ecuación quedara de la siguiente forma:
2X-4=0
Despejando tenemos que X=2
Ahora reemplazamos el valor de X=2 en la siguiente ecuación 3^X – 1 con lo que tendremos:
3^2 – 1
9-1
Por lo que 3^X – 1= 8
HAGA CLICK PARA VER 100 EJERCICIOS DE ALGEBRA
Ejercicio 2 simplificar las fracciones:

Calcula 2^X – 3^X
Si 5^(X+3)*5^(X-1)=3^0
Primero despejaremos X de la siguiente ecuación 5^(X+3)*5^(X-1)=3^0. Como las bases son iguales al multiplicar ambos términos se sumaran los exponentes teniendo 5^(2X+2)=3^0. Ahora se tiene 3^0 en la parte derecha pero se buscara que todas las bases sean iguales por lo que expresaremos en términos de 5^0 sin modificar el resultado final ya que ambos valores dan 1. Ahora queda la ecuación de la siguiente forma 5^(2X+2)=5^0.
Como las bases son iguales, los exponentes también serán iguales por lo que la ecuación quedara de la siguiente forma:
2X+2=0
Despejando tenemos que X=-1
Ahora reemplazamos el valor de X=-1 en la siguiente ecuación 2^X – 3^X con lo que tendremos:
2^-1 – 3^-1
(1/2)-(1/3)
(3/6)-(2/6)
Por lo que 2^X – 3^X = 1/6
HAGA CLICK PARA VER EJERCICIOS DE TRIGONOMETRIA
Ejercicio 3: Simplificar la siguiente expresión [5^(a+2)-5^(a-1)]/[5^(a-5)-5^(a-2)]
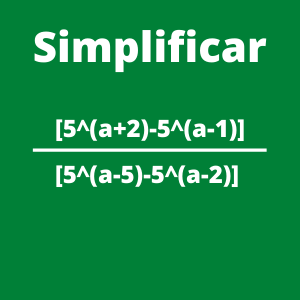
Primero simplificaremos el numerador de la expresión [5^(a+2)-5^(a-1)]. Inicialmente lo separaremos en diferentes términos quedando [(5^a)*(5^2)-(5^a)*(5^-1)]. Ahora factorizaremos 5^a por lo que tendremos: [(5^a)(25-1/5)].
Posteriormente simplificaremos el denominador de la expresión [5^(a-5)-(5^(a-2)]. Primero lo separaremos en diferentes términos quedando [(5^a)*(5^-5)-(5^a)*(5^-2)]. Ahora factorizaremos 5^a por lo que tendremos: [(5^a)(5^-5-5^-2)].
Por lo tanto, toda la expresión numerador y denominador quedara de la siguiente forma:
[(5^a)(25-1/5)]/[(5^a)(5^-5-5^-2)]
Ahora eliminamos el 5^a del numerador como del denominador quedando:
[(25-1/5)]/[(5^-5-5^-2)]
Finalmente haciendo calculos a la expresión tendremos:
[(24,8)]/[(0,00032-0,04)]
[(24,8)]/[(-0,003968)]
-625