En trigonometria y geometria (ley de senos) , en la ley de los senos es una relación que existe entre las longitudes de los lados de un triangulo y los senos que hay de sus ángulos opuestos. A partir de dos lados y un ángulo se puede calcular lo demás o con un lado y dos ángulos, tal como se puede observar en los siguientes ejemplos que se presentan a continuación:
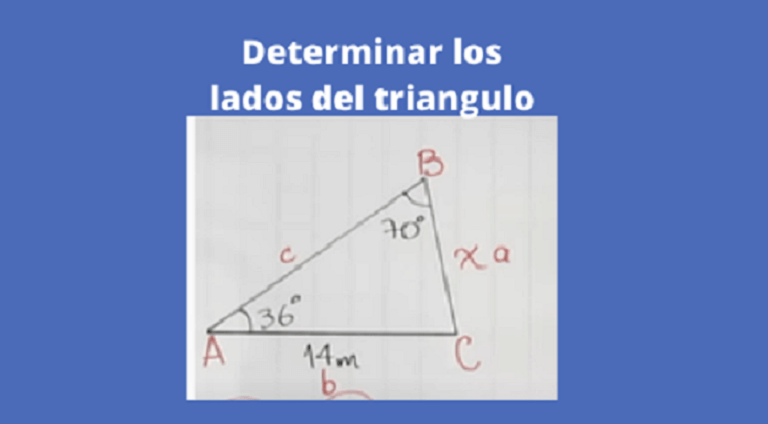
Ejercicio 1 trigonometria y geometria (ley de senos) : Determinar los lados de un triangulo sabiendo que un lado es de 14 m, un ángulo de 70 grados y el otro angulo de 36 grados como se observa en la gráfica.
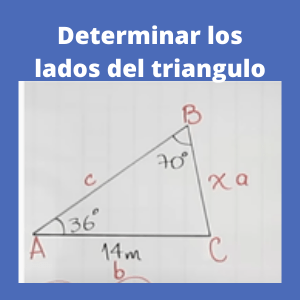
Primeramente se utilizara la siguiente fórmula de la Ley de Senos la cual es la siguiente:
a/sen A = b/senB = c/senC
Calculemos el valor de a. Remplazando los valores tendremos:
a/sen A = b/senB
a/sen 36 = 14/sen 70
Por lo que a será igual a:
a = (14/sen 70)*sen 36
a= 8,75 m
Así mismo para determinar el valor del lado c se deberá realizar lo siguiente:
Calculemos el valor de c. Remplazando los valores tendremos:
c/sen C = b/sen B
Sabemos que la suma de ángulos de un triángulo es de 180 grados. Restando a 180 los otros dos ángulos que tenemos que son de 36 grados y 70 grados, tendremos un ángulo de 74 grados como ángulo C.
c/sen 74 = 14/sen 70
Por lo que a será igual a:
c = (14/sen 70)*sen 74
c= 14,32 m
Ejercicio 2 trigonometria y geometria (ley de senos) : Determinar los lados de un triangulo sabiendo que un lado es de 9 m, un ángulo de 100 grados y el otro angulo de 28 grados como se observa en la gráfica.
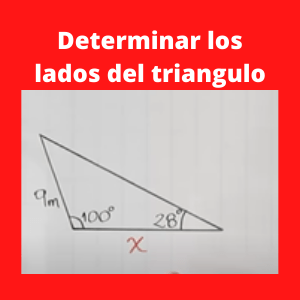
Primeramente se utilizara la siguiente fórmula de trigonometria y geometria (ley de senos) la cual es la siguiente:
a/sen A = b/senB = c/senC
Calculemos el valor de a. Remplazando los valores tendremos:
a/sen A = b/senB
a/sen 100 = 9/sen 28
Por lo que a será igual a:
a = (9/sen 28)*sen 100
a= 18,87 m
Así mismo para determinar el valor del lado c se deberá realizar lo siguiente:
Calculemos el valor de c. Remplazando los valores tendremos:
c/sen C = b/sen B
Sabemos que la suma de ángulos de un triángulo es de 180 grados. Restando a 180 los otros dos ángulos que tenemos que son de 100 grados y 28 grados, tendremos un ángulo de 52 grados como ángulo C.
c/sen 52 = 9/sen 28
Por lo que a será igual a:
c = (9/sen 28)*sen 52
c= 15,1 m
VER EJERCICIOS DE PROGRESIONES
Ejercicio 3: Determinar los lados de un triangulo sabiendo que un lado es de 52 cm, otro lado de 40 cm y un ángulo de 42 grados como se observa en la gráfica.
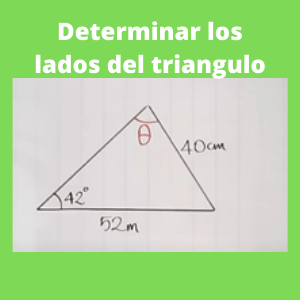
Primeramente se utilizara la siguiente fórmula de trigonometria y geometria (ley de senos) la cual es la siguiente:
a/sen A = b/senB = c/senC
Calculemos el valor de a. Remplazando los valores tendremos:
a/sen A = b/senB
40/sen 42 = 52/sen b
Por lo que a será igual a:
sen b = 52/(40/sen 42)
sen b= 0,86987
Por lo que el ángulo b tendra un valor de 60,44
Así mismo para determinar el valor del lado c se deberá realizar lo siguiente:
Calculemos el valor de c. Remplazando los valores tendremos:
c/sen C = b/sen B
Sabemos que la suma de ángulos de un triángulo es de 180 grados. Restando a 180 los otros dos ángulos que tenemos que son de 42 grados y 60,44 grados, tendremos un ángulo de 77,56 grados como ángulo C.
c/sen 77,56 = 40/sen 42
Por lo que a será igual a:
c = (40/sen 42)*sen 77,56
c= 58,37 m
Ejercicio 4: Determinar los lados de un triangulo sabiendo que un lado es de 13 m, un ángulo de 65 grados y el otro angulo de 30 grados como se observa en la gráfica.
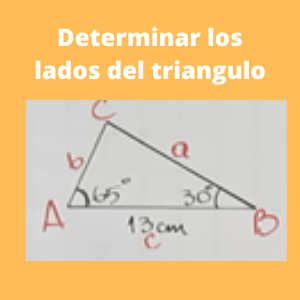
Sabemos que la suma de ángulos de un triángulo es de 180 grados. Restando a 180 los otros dos ángulos que tenemos que son de 65 grados y 30 grados, tendremos un ángulo de 85 grados como ángulo C.
Primeramente se utilizara la siguiente fórmula de trigonometria y geometria (ley de senos) la cual es la siguiente:
a/sen A = b/senB = c/senC
Calculemos el valor de a. Remplazando los valores tendremos:
a/sen A = b/senB
a/sen 65 = 13/sen 85
Por lo que a será igual a:
a = (13/sen 85)*sen 65
a= m
Así mismo para determinar el valor del lado c se deberá realizar lo siguiente:
Calculemos el valor de c. Remplazando los valores tendremos:
c/sen C = b/sen B
13/sen 85 = b/sen 30
Por lo que a será igual a:
b = (13/sen 85)*sen 30
b= 6,52 m