En el presente artículo veremos ejercicios de ángulos de un triángulo. Todos los triángulos tienen tres ángulos. De acuerdo a los ángulos de un triángulo varía su denominación, como ser:
Equilátero: Es cuando todos los ángulos son iguales.
Rectángulo: Si un ángulo es de 90 grados que forma una «L».
Isósceles: Dos ángulos del triángulo son iguales y el tercero es distinto.
Para calcular un ángulo existe la siguiente opción: Conocer dos ángulos del triángulo y encontrar el valor del tercer ángulo, sabiendo que entre los tres suman 180 grados. Esta es la opción que analizaremos en el presente artículo:
A continuación se pueden ver 4 ejercicios para poder determinar los ángulos de un triángulo:
Primero: ejercicios de ángulos de un triángulo

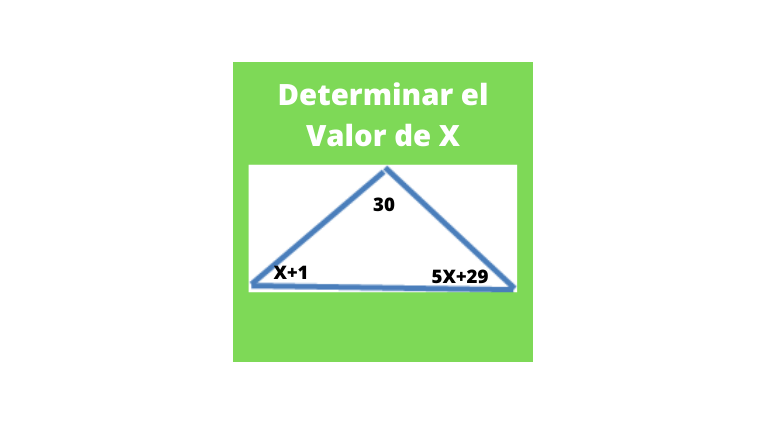
Para calcular X, debemos saber que la suma de todos los ángulos de un triángulo es de 180 grados. Por lo que empezaremos con:
30 + X + 1 + 5X + 29 =180
60 + 6X = 180
6X = 120
X = 20
Por lo tanto el primer ángulo será:
30 grados
El segundo ángulo será:
X + 1 = 20 + 1 = 21 grados
El tercer ángulo será:
29 + 5*X= 29 + 5*20 = 29 + 100 = 129 grados
La suma de todos los ángulos deberá dar 180 grados, aquí tenemos la comprobación:
30 + 21 + 129 = 180 grados
Segundo: ángulos de un triángulo
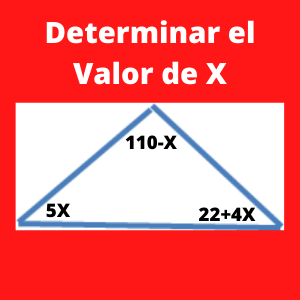
Para calcular X, debemos saber que la suma de todos los ángulos de un triángulo es de 180 grados. Por lo que empezaremos con:
110- X + 5X + 22 + 4X =180
132 + 8X = 180
8X = 48
X = 6
Por lo tanto el primer ángulo será:
110 – X = 104 grados
El segundo ángulo será:
5*X = 5*6 = 30 grados
El tercer ángulo será:
22 + 4*X= 22 + 4*6 = 22 + 24 = 46 grados
La suma de todos los ángulos deberá dar 180 grados, aquí tenemos la comprobación:
104 + 30 + 46 = 180 grados
HAGA CLICK PARA VER EJERCICIOS DE FACTORIZACION
Tercero:ángulos de un triángulo
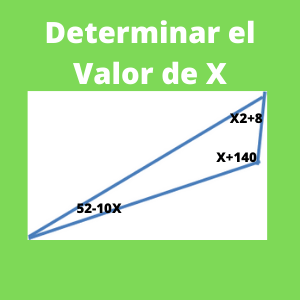
Para calcular X, debemos saber que la suma de todos los ángulos de un triángulo es de 180 grados. Por lo que empezaremos con:
X2 + 8 + 52 – 10X + X + 140 =180
X2 – 9X + 200 =180
X2 – 9X + 20 =0
Factorizando la expresión tenemos:
(X – 5)(X – 4) =0
Por lo que existen dos resultados:
X=5
X=4
Primer resultado X= 5
Por lo tanto el primer ángulo será:
X2 + 8 = 52 + 8 = 33 grados
El segundo ángulo será:
52-10X = 52 – 10*5 = 2 grados
El tercer ángulo será:
X + 140 = 5 + 140 = 145 grados
La suma de todos los ángulos deberá dar 180 grados, aquí tenemos la comprobación:
33 + 2 + 145 = 180 grados
Segundo resultado X = 4
Por lo tanto el primer ángulo será:
X2 + 8 = 42 + 8 = 24 grados
El segundo ángulo será:
52-10X = 52 – 10*4 = 12 grados
El tercer ángulo será:
X + 140 = 4 + 140 = 144 grados
La suma de todos los ángulos deberá dar 180 grados, aquí tenemos la comprobación:
24 + 12 + 144 = 180 grados
X+15
2X+6
4X-2
Cuarto: ángulos de un triángulo
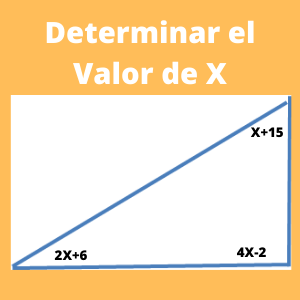
Para calcular X, debemos saber que la suma de todos los ángulos de un triángulo es de 180 grados. Por lo que empezaremos con:
X+15 + 2X + 6 + 4X -2 =180
19 + 7X = 180
7X = 161
X = 23
Por lo tanto el primer ángulo será:
X+ 15 = 38 grados
El segundo ángulo será:
2*X + 6 = 2*23 + 6 = 52 grados
El tercer ángulo será:
4X-2= 4*23 – 2 = 92 – 2 = 90 grados
La suma de todos los ángulos deberá dar 180 grados, aquí tenemos la comprobación:
38 + 52 + 90 = 180 grados