La combinatoria es una especialidad en el campo de la matemática correspondiente al área de matemáticas discretas que estudia la enumeración y creación.
A continuación se pueden apreciar los siguientes ejercicios de combinatoria:
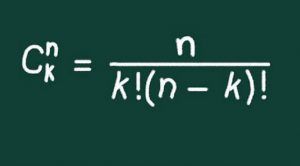
Ejercicios de Combinatoria
Permutación versus combinación
¿Qué son combinaciones? Resolvamos ejercicios
Ejercicios de Combinatoria
Permutación versus combinación
¿Qué son combinaciones? Resolvamos ejercicios
La Combinatoria es la porción de las Matemáticas que estudia las múltiples maneras de hacer agrupaciones con los recursos de un grupo, formándolas y calculando su número. Además, estudia las ordenaciones o agrupaciones de un definido número de recursos.
La Combinatoria es un instrumento que nos posibilita contar el número de situaciones que tienen la posibilidad de ofrecer al dominar a un grupo limitado a las actividades de ordenar y/o escoger entre sus recursos.
La combinatoria es una especialidad en el campo de la matemática que es utilizada en apuestas hoy en día. Para lograr ejercer la combinatoria primero debemos conocer los conceptos básicos de combinatoria, como por ejemplo permutaciones, variaciones, etcétera.
Características de los números combinatorios: Números combinatorios complementarios son esos que poseen el mismo numerador y la suma de sus directivas es lo mismo al numerador.
Con base en el latín combinatio, mezcla es un vocablo que refiere al acto y efecto de combinar algo o de combinarse (es mencionar, juntar, complementar o ensamblar cosas distintas para poder hacer un compuesto).
Qué significa combinaciones en Matemáticas. Se denomina combinaciones de m recursos tomados de n en n (m ≥ n) a cada una de las agrupaciones probables que tienen la posibilidad de hacerse con los m recursos de manera que: No acceden todos los recursos. No importa el orden.
Generalmente la teoria combinatoria es de gran utilidad en esas superficies donde diversas formas de agrupar un numero limitado de recursos tenga trascendencia. En la investigación combinatorio se distinguen las variaciones, las permutaciones y las combinaciones.
Los inconvenientes de combinatoria aparecen a menudo en las olimpiadas matemáticas. Son inconvenientes donde se encuentra la proporción de objetos que tienen una cierta propiedad; es decir, se debe contar. En el problema que presentamos posteriormente realizamos un conteo usando el inicio de multiplicación.