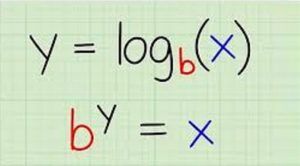Una vez que a mí me enseñaron los logaritmos, no recuerdo que me contasen para qué servían, me explicaron su definición, así como una secuencia de normas para lograr operar con ellos, o sea, aprendí puro cálculo sin ni una idea de comprensión de lo cual estaba realizando, ahora lo recuerdo y pienso que faltó que esto además me lo enseñasen para lograr verle utilidad a todo lo aprendido.
Anterior a contar para que sirven, hagamos un breve repaso de ellos, debido a que nos permitirá entenderlo todo mejor.
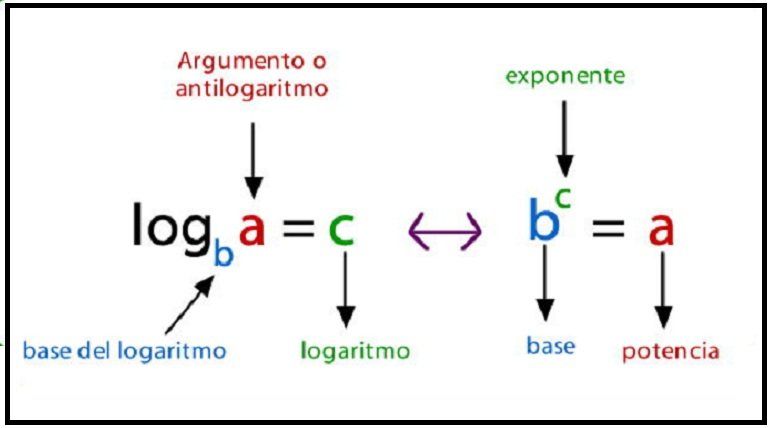
Un logaritmo es el exponente al que se debe elevar un número, denominado base, para obtener otro número definido. El logaritmo con base 10 de 1000 es 3.
logab=c ⇔ ac=blogab=c ⇔ ac=b
ó
siendo por definición {b∈R:b>0} y {a∈R-{1}:a>0} siendo por definición {b∈R:b>0} y {a∈R-{1}:a>0}
El procedimiento logarítmico ha sido presentado públicamente por el matemático y teólogo escocés John Napier en 1614, en un libro titulado «Mirifici Logarithmorum Canonis Descriptio» (Descripción de una maravillosa tabla de Logaritmos), en dicha etapa los trabajos científicos se escribían todos en latín. De Napier viene el nombre de logaritmo neperiano (Napierian logarithm o Naperian logarithm).
¿Qué es una función logarítmica?
Logaritmo 100
3 Ejercicios de logaritmos de base 10
Es primordial rememorar varias características de los logaritmos para comprender para que sirven:
Logaritmo de un producto.
El logaritmo de un producto es igual a la suma de los logaritmos de los componentes.
logba⋅c=logba+logbclogba⋅c=logba+logbc
Logaritmo de un cociente.
El logaritmo de un cociente es lo mismo al logaritmo del dividendo, menos el logaritmo del divisor.
logbac=logba−logbclogbac=logba−logbc
Logaritmo de una potencia.
logbcn=nlogbclogbcn=nlogbc
Logaritmo de una raíz
logaxm−−−√n=mnlogaxlogaxmn=mnlogax
El antilogaritmo: El antilogaritmo nos posibilita desde la base y del exponente calcular el argumento (lo opuesto que el logaritmo que desde la base y el argumento nos da el exponente).
log28=3log28=3
siendo 2 la base, 8 el argumento y 3 el exponente.
Permite desde la base y del exponente, obtener el argumento.
antilog 2 3=8
Los logaritmos se emplearon primordialmente como un instrumento para lograr simplificar multiplicaciones, divisiones y la sustracción de radicales una vez que teníamos que laborar con números bastante bastante gigantes.
A partir de mediados del siglo XX con la extensión de los ordendores de manera más generalizada, esto ya ha perdido algo de sentido pues dichos realizan aquellos cálculos gigantes de una manera simple, sin embargo Anteriormente, como los pcs no eran tan disponibles, si teníamos que laborar con cifras bastante gigantes, la solución era usar logaritmos y tablas de logaritmos (así como de tablas de antilogaritmos) en las que poder consultar el costo del logaritmo de un número.
Los logaritmos nos permiten cambiar el producto en una suma (primera de las características de los logaritmos que hemos repasado, es más simple sumar que multiplicar), el cociente en resta (es más simple restar que dividir), una potencia en una multiplicación y una raíz en una fácil separación.
Con la realidad de tablas de logaritmos para obtener el logaritmo de un número fácilmente (y su antilogaritmo), lo cual hacíamos era en vez de laborar con números monumentales, laborar con el logaritmo de aquellos números que eran cosas bastante más pequeñas
log10100000000=8log10100000000=8
mejor laborar con el 8 que con 100000000 y finalmente del proceso calculábamos el antilogaritmo de lo obtenido.
¿Qué es una función logarítmica?
Logaritmo 100
Ejercicios de logaritmos
3 Ejercicios de logaritmos de base 10