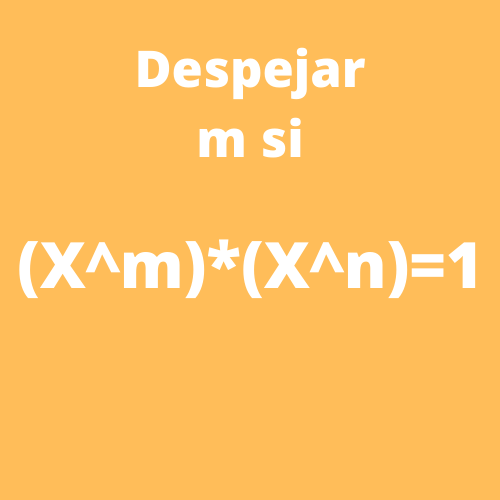Como resolver operaciones algebraicas de potencias. Las potencias son utilizadas con la finalidad de escribir de forma simplificada una multiplicación formada por varios números iguales. Por ejemplo, 5 x 5 x 5 x 5. Estamos multiplicando 4 veces el número 5. Para ponerlo en forma de potencia escribimos primero el 5 y arriba a la derecha escribimos el 4 en pequeño.
Al multiplicar potencias de igual base, mantendremos la base y sumaremos los exponentes. Cuando queremos dividir potencias de igual base, mantendremos la base y restaremos los exponentes. Para resolver la potencia de una potencia, debemos mantener la base y multiplicar los exponentes.
A continuación se pueden apreciar 3 ejercicios de operaciones algebraicas:
Ejercicio 1: Despejar m si (X^m)*(X^n)=1
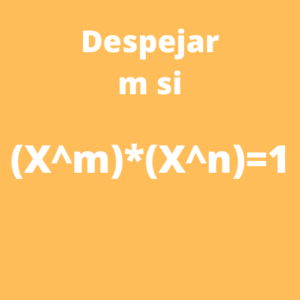
Para determinar el valor de m de la siguiente ecuación (X^m)*(X^n)=1, primero realizamos la multiplicación sabiendo que en potencias con bases iguales se pone la misma base se suman los exponentes por lo que tendremos X^(m+n)=1. Ahora buscamos que todos los términos de la ecuación tengan la misma base quedando X^(m+n)=X^0. Finalmente como las bases son iguales también serán los exponentes por lo que el resultado es m+n=0 o también m=-n.
VER EJERCCIOS DE SISTEMAS DE ECUACIONES
Ejercicio 2 como resolver operaciones algebraicas: Despejar m si [X^(m+3)]*[X^(n-1)]=1

Para determinar el valor de m de la siguiente ecuación [X^(m+3)]*[X^(n-1)]=1, primero realizamos la multiplicación sabiendo que en potencias con bases iguales se pone la misma base se suman los exponentes por lo que tendremos X^(m+3+n-1)=1. Ahora buscamos que todos los términos de la ecuación tengan la misma base quedando X^(m+n+2)=X^0. Finalmente como las bases son iguales también serán los exponentes por lo que el resultado es m+n+2=0 o también m=-n-2.
Ejercicio 3: Despejar m si [X^(m+7)]*[X^(n-2)]=1

Para determinar el valor de m de la siguiente ecuación [X^(m+7)]*[X^(n-2)]=1, primero realizamos la multiplicación sabiendo que en potencias con bases iguales se pone la misma base se suman los exponentes por lo que tendremos X^(m+n+7-2)=1. Ahora buscamos que todos los términos de la ecuación tengan la misma base quedando X^(m+n+5)=X^0. Finalmente como las bases son iguales también serán los exponentes por lo que el resultado es m+n+5=0 o también m=-n-5.