Inicialmente calculamos potencias aplicando la definición de la operación de potenciación, después explicaremos y aplicaremos las siguientes propiedades de potencias:
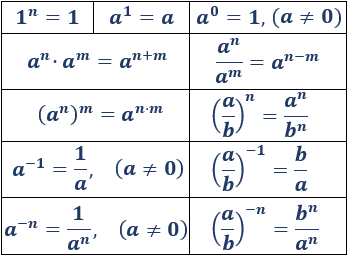
La potencia an representa el producto que tiene n veces el número a. El número a se llama base y el número n se llama exponente.
Ejemplo1 : potencias de 2:
2^1=2
2^2=2*2=4
2^3=2*2*2=8
2^4=2*2*2*2=16
Ejemplo 2: Diferentes potencias
Calcular las potencias 3^2, 5^3, 11^1, 7^0, 1^22, 6^2 y 0^20.
Solución
La potencia 3^2 (tres al cuadrado) es el producto de dos treses:
3^2 = 3*3=9
La potencia 5^3 (cinco al cubo) es el producto de tres cincos:
5^3 = 5*5*5=125
La potencia 11^1 (once elevado a uno) es el producto de un once:
11^1=11
La potencia 7^0 (siete elevado a cero) es el producto de cero sietes:
7^0=1
La potencia 1^22 (uno elevado a veintidós) es el producto de veintidós unos:
1^22=1*1*1*1—–=1
La potencia 6^2 (seis al cuadrado) es el producto de dos seises:
6^2=6*6=36
La potencia 0^20 (cero elevado a veinte) es el producto de veinte ceros:
0^20=0*0*0*0….=0
Por lo que hemos visto, podemos decir:
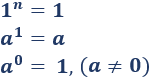
Dicho en palabras,
- Si la base de una potencia es 1, el resultado es 1.
- Si el exponente de una potencia es 1, el resultado es la base.
- Si el exponente de una potencia es 0 (y la base no es 0), el resultado es 1.
Problema 2
Calcular las siguientes potencias de números negativos: (−1)^2, (−2)^3, (−5)^2 y (−1)^5.
Ayuda: utilizar la regla de los signos (el producto de números con el mismo signo es un número positivo y el producto de números con signos distintos es un número negativo).
Solución
La potencia (−1)^2 es el producto de dos unos negativos:
(−1)^2=
(−1)*(-1)=
=1
La potencia (−2)^3 es el producto de tres doses negativos:
(−2)^3=
(−2)*(−2)*(−2)^3=
=-8
La potencia (−5)^2 es el producto de dos cincos negativos:
(−5)^2=
(−5)*(−5)=
=25
La potencia (−1)^5 es el producto de cinco unos negativos:
(−1)^5=
(−1)*(−1)*(−1) *(−1) *(−1)=
=-1
Observad que si la base de una potencia es negativa:
- El resultado es positivo si el exponente es par.
- El resultado es negativo si el exponente es impar.
Esto puede resumirse como:
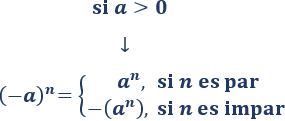
Problema 3
Determinar (−3)^3 y (−5)^2.
Solución
La potencia (−3)^3 es el producto de tres treses negativos:
(−3)^3=
(−3)*(−3)*(−3)=
=-27
La potencia (−5)^2 es el producto de dos cincos negativos:
(−5)^2=
=(−5)*(−5)=
= 25 = 5^2
Exponente negativo
La potencia de un número distinto de 0 elevado a -1 es igual a su inverso:
![]()
La potencia de un número distinto de 0 elevado al número negativo −n es el inverso del número elevado a^n:
![]()
Problema 4
Calcular las siguientes potencias con exponente negativo:
7^-1
5^-2
2^-3
(-3)^-2
(-1)^-5
(-2)^-3
Solución
La potencia 7^−1 es el inverso de 7:
7^-1 = 1/7
La potencia 5^−2 es el inverso de 5^2:
5^-2 =(1/5^2)= 1/25
La potencia 2^−3 es el inverso de 2^3:
2^-3= 1/(2^3) =1 /8
La potencia (−3)^−2 es el inverso de (−3)^2:
(-3)^-2 = 1/(-3)^2 = 1/9
La potencia (−1)^−5 es el inverso de (−1)^5:
(−1)^−5 = 1/(−1)^5
1/−1= −1
La potencia (−2)^−3 es el inverso de la potencia (−2)^3:
(−2)^−3 = 1/(−2)^3
= 1/-8 = -1/8
Producto y cociente de potencias
El producto de dos potencias con la misma base es la potencia de dicha base y cuyo exponente es la suma de los exponentes:
![]()
El cociente de dos potencias con la misma base es la potencia de dicha base y cuyo exponente es la resta de los exponentes:
![]()
Problema 5
Calcular los siguientes productos de potencias:
2^2*2^2=
5^4*5^-1*5^2*5^-3=
2^2*3^2*2=
5^5 * 2^2 * 3^-1 * 5^-3 * 2^2 * 3=
Los dos primeros productos se calculan rápidamente. El primero es el producto de dos potencias con base 2:
2^2*2^2=
2^(2+2)=
2^4=16
El segundo es el producto de cuatro potencias con base 5:
5^4*5^-1*5^2*5^-3=
5^(4-1+2-3)=
5^2=25
En el tercero tenemos dos bases distintas:
2^2 * 3^2 * 2=
2^(2+1)* 3^2=
2^3 * 3^2=
8*9=72
En el cuarto tenemos tres bases distintas:
5^5 * 2^2 * 3^-1 * 5^-3 * 2^2 * 3=
5^(5-3) * 2^(2-2) * 3^(-1+1) =
5^2 * 2^0 * 3^0 =
25*1*1=
25

