El asunto de perimetros y area de triangulos es primordial en la Geometría, aprender sus características, teoremas y fórmulas es imprescindible.
En este artículo, te enseñare cómo se resuelven los ejercicios de triángulos con procedimientos fáciles para que puedas comprenderlo de forma sencilla.
En los ejercicios aplicaremos las características principales del triángulo, así como observaremos cómo encontrar el perímetro y el área de un triángulo.
Recordamos algunos conceptos que son importantes para lograr ejercicios resueltos de area de triangulos como son los vertices, la altura y la base los mismos que se encuentran en el presente artículo.
- Un triángulo tiene ese nombre porque está compuesto por tres lados.
- Se denominan vértices a la intersección entre un lado y otro del triángulo.
- La altura es la línea de la recta que es perpendicular a la altura.
- La base de un triángulo, puede ser cualquiera de los tres lados, depende como miremos el triángulo, cuando determinamos la base la altura es la perpendicular a la misma.
El área de un triángulo se calcula mediante un proceso diferente según el tipo de triángulo en cuestión o los elementos conocidos del triángulo.
La fórmula general para calcular el área de cualquier triángulo es:
Área = b * h / 2
Dónde está:
b = base
h = altura
La forma de calcular ejercicios de triangulos para quinto de primaria es la siguiente:
Área del triángulo equilátero
Un triángulo equilátero tiene los tres lados iguales. Como con cualquier triángulo, su área será la mitad de la altura de la base (a). En un triángulo equilátero, se define mediante la siguiente fórmula:
Área = (Raíz(3)*a^2)/4
Dónde está:
a = lado del triángulo
Este tipo de ejercicios de triangulos para primaria son los más utilizados.
Área del triángulo isósceles
Otro triangulo muy utilizado en ejercicios con triangulos para primaria es el triangulo isóceles. Como con cualquier triángulo, el área de un triángulo isósceles será la mitad de la altura de la base (b). En un triángulo isósceles, su fórmula de cálculo es la siguiente:
Área = (b/2)(Raíz(a^2-0,25*b^2))
Dónde está:
a = uno de los equiláteros
b = el otro lado del triángulo.
Área de un triángulo escaleno
Si se conocen todos los lados (a,b y c), se puede usar la fórmula de Heron para calcular el área de ese tipo de triángulo, muy utilizado para ejercicios de geometria para quinto grado de primaria, donde el área es:
Área = Raíz((s)(s-a)(s-b)(s-c))
Dónde está: a, b, c = tres lados del triángulo s = medio perímetro del triángulo.
S=(a+b+c)/2
Si conoce el borde (b) y la altura (h) asociados con el borde, también puede calcularlo. Área= b*h/2
Dónde está:
b=base
h=altura
Área del triángulo rectángulo
Un triángulo rectángulo tiene un ángulo recto (90º), por lo que su altura es la misma que uno de sus lados (a), como se vee en este tipo de triángulos se utiliza como ejercicios de angulos interiores de un triangulo para primaria.
El área es la mitad del producto de los dos lados que forman un ángulo recto.
Área=b*h/2
Dónde está:
b=base
h=altura
Área triangular con ángulo y altura de base conocidos
El área de cualquier triángulo se puede calcular conociendo un lado y la altura asociada con ese lado. Este aspecto sirve de base.
Su área será la mitad del producto de la base (b) y la altura (h).
Área=b*h/2
Dónde está:
b=base
h=altura
A continuación se pueden observar algunos ejercicios con triangulos para primaria:
Ejercicios de Triangulos para Primaria
Ejercicio 1: area del triangulo
En la figura mostrada se exige encontrar el ángulo «x».
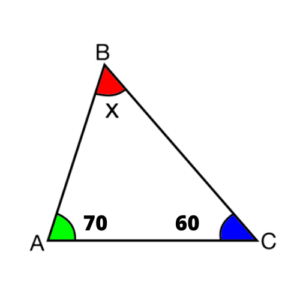
Solución:
Debemos conocer una propiedad que se cumple en un triángulo:
«Los suma de los ángulos internos en un triángulo es 180°»
Aplicando esta propiedad en la figura del problema tendremos:
70° + 60° + x = 180°
Resolviendo esta ecuación:
130° + x = 180°
Despejando x, obtendremos:
x = 180° – 130°
Por lo tanto, x = 50°
Además, tenemos la posibilidad de mencionar que el triángulo dado es un triángulo agudo (sus ángulos internos son menores que 90°).
Ejercicio 2: area del triangulo
En la figura se exige calcular el costo del ángulo «θ».
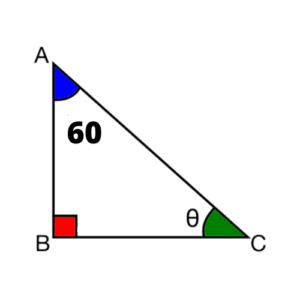
Solución:
Por la misma propiedad que aplicamos al anterior problema, es decir que la suma de los ángulos es de 180 grados, mencionamos:
90° + 60 + θ = 180°
⇒ θ = 180° – 150°
Por lo que el resultado final será de θ=30°
Ejercicio 3:
En un triángulo sus lados miden 18cm, 14cm y 22cm respectivamente. Calcular el perímetro del triángulo.
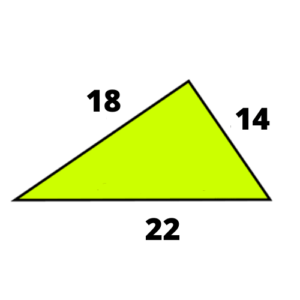
Solución:
Dibujamos el triángulo con sus medidas.
Una vez que nos piden calcular o sacar el perímetro de un triángulo, en verdad lo cual nos piden es la suma de los lados del triángulo.
Entonces:
Perímetro del triángulo = 18cm + 14cm + 22cm
Por lo tanto el perímetro del triangulo es, Perímetro del triángulo = 54cm
Ejercicio 4:
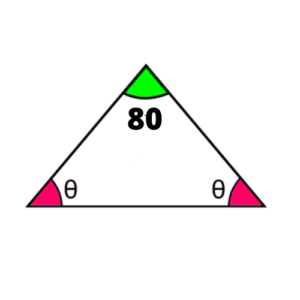
El ángulo desigual de un triángulo isósceles mide 80°. ¿Cuánto mide uno de los ángulos congruentes?
Solución:
Veamos el dibujo del triángulo isósceles según los datos del ejercicio:
Luego mencionamos:
870° + θ + θ = 180°
2θ = 180° – 80° = 100°
Por lo tanto, el ángulo buscado es de θ = 50°
Ejercicio 5:
Existe un teorema conocido por bastante más tiempo que 3mil años y que todavía, actualmente, lo seguimos usando gracias a su trascendencia en las matemáticas, nos referimos al teorema de Pitágoras.
El teorema de Pitágoras sugiere que en un triángulo rectángulo se cumple que: La suma al cuadrado de los catetos es equivalente al cuadrado de la hipotenusa.
La siguiente figura queda mostrado cómo se aplica este teorema.
En el triángulo rectángulo de la figura los catetos son a y b y la hipotenusa c. Entonces se cumple la fórmula de Pitágoras:
c² = a² + b²
Está formula usaremos una vez que nos pidan encontrar la hipotenusa o cualquier cateto conociendo los demás 2 lados del triángulo rectángulo.
Por ejemplo:
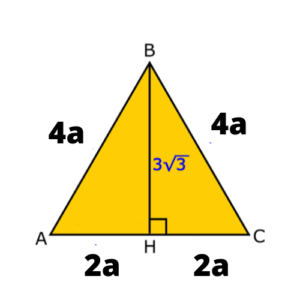
En un triángulo equilátero se traza la elevación cuya medida es 3√3u, calcular el perímetro de hablado triángulo.
Solución:
Por ver ahora un triángulo equilátero de vértices A, B y C y Elevación BH.
Nos piden determinar:
Perímetro del Triángulo Equilátero = 4a + 4a + 4a = 12a
Entonces, pero como hacemos ahora para calcular el área, tendremos que utilizar el Teorema de Pitágoras:
(4a)² = (2a)² + (3√3)²
⇒ 16a² = 4a² + 27 ⇒ 12a² = 27
⇒ a = Raiz(27/12)
Reemplazando los valores tenemos que:
Perímetro del Triángulo Equilátero = 12(Raiz(27/12))
Área del triángulo equilátero es = b*h = b*h = 2a*3√3= a*6√3= (Raiz(27/12))*6√3
Ejercicios de angulos de triángulos para secundaria
A continuación se pueden observar ejercicios de area de triangulos:
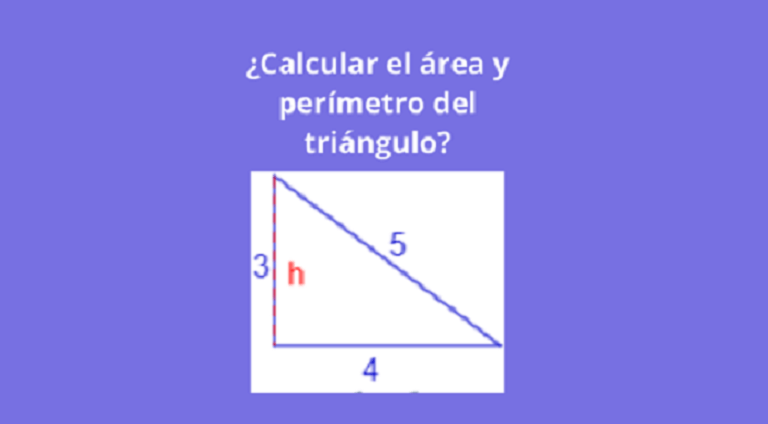
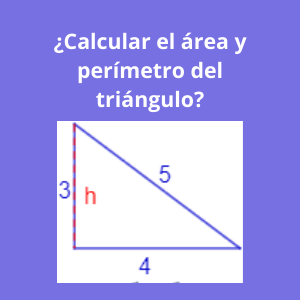
Ejercicio 1 area de triangulos : ¿Calcular el área y perímetro del triángulo?
Para calcular el área del triángulo se utilizara la siguiente fórmula:
A= (b*h)/2
Sabemos que la base es 4 y la altura es 3, por lo cual tendremos:
= (4*3)/2
= 12/2 = 6
El perímetro de un triángulo es la suma de las longitudes de sus tres lados, por lo que el perímetro del triángulo rectángulo de lados 3, 4 y 5 es 12
Otros ejercicios para calcular el area del triangulo se pueden observar a continuación:
Ejercicio 2 area de triangulos: ¿Calcular el área del triángulo obtusángulo?
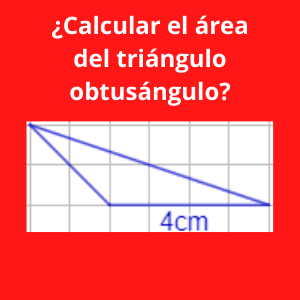
Observando la cuadrícula y comparando la misma con la base que es de 4, podemos ver que cada cuadrado es de 1 cm, por lo que la altura del triángulo será de 2 cm.
Como conocemos la altura y la base del triángulo, podemos calcular el área a partir de la siguiente fórmula:
A= (b*h)/2
= (4*2)/2 = 4
Por lo que el área del triángulo será de 4cm2.
Ejercicio 3 area de triangulos: ¿Calcular el área del siguiente triangulo?
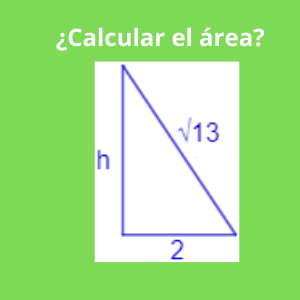
El presente ejercicio es un triángulo rectángulo, donde conocemos uno de sus catetos que mide 2 cm cm y la hipotenusa que mide Raíz(13).
Para calcular el área del triángulo, se necesita saber el valor del otro cateto, que en este caso viene a ser la altura del triángulo. Al ser un triángulo rectángulo se puede aplicar el teorema de Pitágoras.
El teorema de Pitágoras dice que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de sus catetos. Por tanto, en el siguiente triangulo tendremos:
(RAIZ(13))2 = h2 + 22
13 = h2 + 4
h2 = 13 – 4
h2 = 9
Hacemos la raíz cuadrada:
h2 = 9
h = Raiz(9)
h = 3
Por tanto, la altura de triángulo es 3 cm.
Al tener la altura, ya podremos calcular el area del triangulo:
A= (b*h)/2 = (2*3)/2 = 3
Por lo que, el área del triángulo es de 3 cm2.
HAGA CLICK AQUI PARA VER COMO RESOLVER FRACCIONES
Ejercicio 4 area de triangulos: ¿Calcular el área del triángulo equilátero?
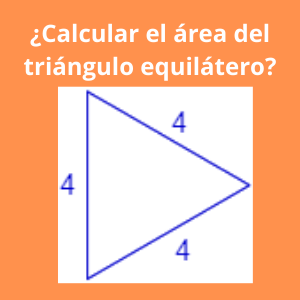
Los problemas de area de triangulos con referencia al triangulo equilatero se puede ver en el siguiente ejemplo. De cada triangulo pequeño tendremos un lado de 2 cm y el otro lado de 4 cm. Utilizando la fórmula de Pitágoras se podrá obtener el valor del tercer lado siendo este de:Este ejemplo se refiere a un triángulo equilátero, es decir que los tres lados son iguales. Podemos calcular la altura por el teorema de Pitágoras, dividiendo el triángulo en dos triángulos más pequeños.
42 = h2 + 22
16 = h2 + 4
12 = h2
Raiz(12) = h
Por tanto, la altura de triángulo es Raiz(12) cm.
Al tener la altura, ya podremos calcular el area de triangulos:
A= (b*h)/2 = 2*Raiz(12)/2 = Raiz(12)
Por lo que, el área del triángulo es de Raiz(12) cm2, lo que es igual a 3,46 cm2.
Al ser dos triángulos del mismo tamaño, se multiplicara por 2 obteniendo un área del triángulo grande de 6,928 cm2.
Espero que te haya gustado los diferentes ejercicios de areas de triangulos que mostramos en el presente artículo.