La trigonometria es una parte de las matemáticas, que se ocupa de determinar los ángulos y lados de un triángulo. La forma de medir la trigonometría es a través del seno, coseno; tangente, cotangente; secante y cosecante.
La trigonometria es utilizada en muchas ciencias tales como la astronomía para medir distancias a estrellas y en la geografía para medir distancias entre puntos geográficos. A continuación se pueden apreciar tres ejercicios de trigonometría donde se aplican la Ley de Senos y Ley de Cosenos:
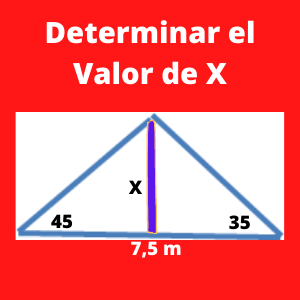
Ejercicio 1 trigonometria: Calcular la altura (h) del siguiente triángulo:
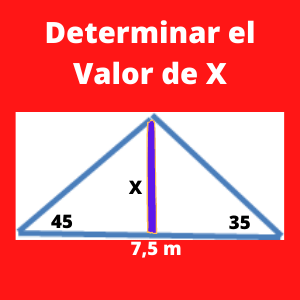
Sabemos que la suma de ángulos de un triángulo es de 180 grados. Restando a 180 los otros dos ángulos que tenemos que son de 45 grados y 35 grados, tendremos un ángulo de 100 grados como ángulo C.
Primeramente se utilizara la siguiente fórmula de la Ley de Senos para determinar la longitud de los otros dos lados, la cual es la siguiente:
a/sen A = b/senB = c/senC
Calculemos el valor de a. Remplazando los valores tendremos:
a/sen A = b/senB
a/sen 35 = 7,5/sen 100
Por lo que a será igual a:
a = (7,5/sen 100)*sen 35
a= 4,37 m
Así mismo para determinar el valor del lado c se deberá realizar lo siguiente:
Calculemos el valor de c. Remplazando los valores tendremos:
c/sen C = b/sen B
7,5/sen 100 = b/sen 45
Por lo que a será igual a:
b = (7,5/sen 100)*sen 45
b= 5,38 m
Con eso ya se cuenta con la dimensión de los tres lados del triángulo. A su vez ese triángulo se divide en dos por una línea representada por X. Como conocemos el valor de un lado y dos ángulos de un triángulo podremos determinar el valor de X, para lo cual realizaremos el siguiente cálculo para trigonometria:
Aplicación de Funciones Trigonométricas para determinar X
Las funciones trigonométricas utilizadas en triángulos rectángulos son las siguientes:
Sen A= Cateto Opuesto/hipotenusa
Cos A= Catetºo adyacente/hipotenusa
Tang A= Cateto Opuesto/Cateto adyacente
Para calcular X (cateto opuesto), se tienen los siguientes datos:
Hipotenusa = 4,47 m
Angulo = 45
A partir de los datos que tenemos utilizaremos la siguiente fórmula:
Cateto Opuesto = hipotenusa*sen45
Obteniendo el siguiente valor para X:
X = Cateto Opuesto = 4,47*sen45 =3,16
HAGA CLICK PARA VER TODO TIPO DE EJERCICIOS DE MATEMATICAS
Ejercicio 2 : Calcular la altura (h) del siguiente triángulo:
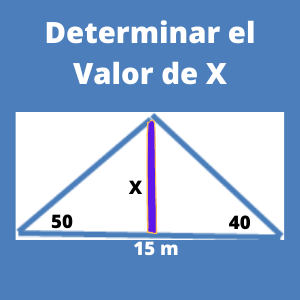
Sabemos que la suma de ángulos de un triángulo es de 180 grados. Restando a 180 los otros dos ángulos que tenemos que son de 50 grados y 40 grados, tendremos un ángulo de 90 grados como ángulo C.
Primeramente se utilizara la siguiente fórmula de la Ley de Senos para determinar la longitud de los otros dos lados, la cual es la siguiente:
a/sen A = b/senB = c/senC
Calculemos el valor de a. Remplazando los valores tendremos:
a/sen A = b/senB
a/sen 40 = 15/sen 90
Por lo que a será igual a:
a = (15/sen 90)*sen 40
a= 9,64 m
Así mismo para determinar el valor del lado c se deberá realizar lo siguiente:
Calculemos el valor de c. Remplazando los valores tendremos:
c/sen C = b/sen B
15/sen 90 = b/sen 50
Por lo que a será igual a:
b = (15/sen 90)*sen 50
b= 11,49 m
Con eso ya se cuenta con la dimensión de los tres lados del triángulo. A su vez ese triángulo se divide en dos por una línea representada por X. Como conocemos el valor de un lado y dos ángulos de un triángulo podremos determinar el valor de X, para lo cual realizaremos el siguiente cálculo para trigonometria:
Aplicación de Funciones Trigonométricas para determinar X
Las funciones trigonométricas utilizadas en triángulos rectángulos son las siguientes:
Sen A= Cateto Opuesto/hipotenusa
Cos A= Catetºo adyacente/hipotenusa
Tang A= Cateto Opuesto/Cateto adyacente
Para calcular X (cateto opuesto), se tienen los siguientes datos:
Hipotenusa = 9,64 m
Angulo = 50
A partir de los datos que tenemos utilizaremos la siguiente fórmula:
Cateto Opuesto = hipotenusa*sen50
Obteniendo el siguiente valor para X:
X = Cateto Opuesto = 9,64*sen50 =7,39
HAGA CLICK PARA VER ACERTIJOS DE MATEMATICAS
Ejercicio 3: Calcular la altura (h) del siguiente triángulo:
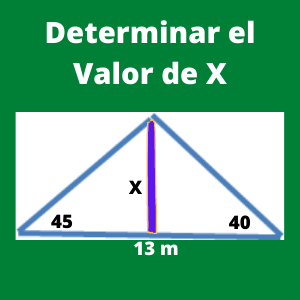
Sabemos que la suma de ángulos de un triángulo es de 180 grados. Restando a 180 los otros dos ángulos que tenemos que son de 45 grados y 40 grados, tendremos un ángulo de 95 grados como ángulo C.
Primeramente se utilizara la siguiente fórmula de la Ley de Senos para determinar la longitud de los otros dos lados, la cual es la siguiente:
a/sen A = b/senB = c/senC
Calculemos el valor de a. Remplazando los valores tendremos:
a/sen A = b/senB
a/sen 45 = 13/sen 95
Por lo que a será igual a:
a = (13/sen 95)*sen 45
a= 9,23 m
Así mismo para determinar el valor del lado c se deberá realizar lo siguiente:
Calculemos el valor de c. Remplazando los valores tendremos:
c/sen C = b/sen B
13/sen 95 = b/sen 40
Por lo que a será igual a:
b = (13/sen 95)*sen 40
b= 8,39 m
Con eso ya se cuenta con la dimensión de los tres lados del triángulo. A su vez ese triángulo se divide en dos por una línea representada por X. Como conocemos el valor de un lado y dos ángulos de un triángulo podremos determinar el valor de X, para lo cual realizaremos el siguiente cálculo:
Aplicación de Funciones Trigonométricas para determinar X
Las funciones trigonométricas utilizadas en triángulos rectángulos son las siguientes:
Sen A= Cateto Opuesto/hipotenusa
Cos A= Catetºo adyacente/hipotenusa
Tang A= Cateto Opuesto/Cateto adyacente
Para calcular X (cateto opuesto), se tienen los siguientes datos:
Hipotenusa = 9,23 m
Angulo = 45
A partir de los datos que tenemos utilizaremos la siguiente fórmula:
Cateto Opuesto = hipotenusa*sen45
Obteniendo el siguiente valor para X:
X = Cateto Opuesto = 9,23*sen45 =6,53
