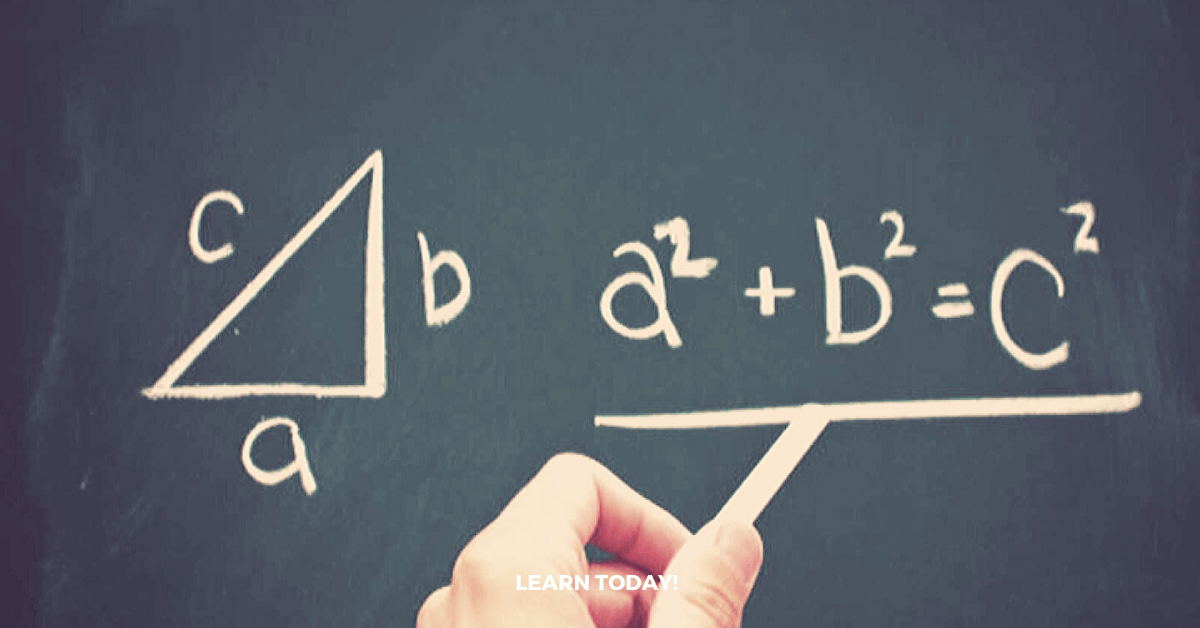
¿Cuáles son las propiedades de los triángulos?
En este artículo, vamos a conocer y comprender la parte de la trigonometria relacionada con cuales son las propiedades de los triangulos y sus tipos. Un triángulo, como su nombre lo indica, es un polígono que tiene tres ángulos.
Entonces, ¿cuándo una figura cerrada tiene tres ángulos?
Cuando tiene tres segmentos de línea unidos de extremo a extremo, ¿verdad?
Por lo tanto, podemos decir que un triángulo es un polígono, que tiene tres lados, tres ángulos y tres vértices.
- Y, la suma de los tres ángulos de cualquier triángulo es igual a 180.
La Fórmula para el área del triángulo es:
Área de cualquier triángulo = ½ * base * altura
Propiedades de los triángulos
Propiedades de los triángulos generales:
Resumamos algunas de las propiedades de los triángulos.
- La suma de todos los ángulos internos de un triángulo es siempre igual a 180. Esto se llama propiedad de suma de ángulos de un triángulo.
- La suma de todos los ángulos exteriores de cualquier triángulo es igual a 360.
- Un ángulo exterior de un triángulo es igual a la suma de sus dos ángulos opuestos interiores.
- La suma de las longitudes de cualquiera de los dos lados de un triángulo siempre es mayor que la longitud del tercer lado.
- Del mismo modo, la diferencia entre las longitudes de los dos lados de un triángulo es siempre menor que la longitud del tercer lado.
- El lado opuesto al ángulo interior más pequeño es el lado más corto y viceversa.
- Del mismo modo, el lado opuesto al ángulo interior más grande es el lado más largo y viceversa.
- La altura de un triángulo es igual a la longitud de la perpendicular caída de un vértice a su lado opuesto, y este lado se considera la base.
- Cualquier ángulo exterior del triángulo es igual a la suma de sus ángulos opuestos interiores. Esto se llama la propiedad del ángulo exterior de un triángulo.
Propiedades de los triángulos fundamentales:
Existen tres propiedades de los triángulos fundamentales, las cuales son las siguientes:
Propiedad 01: Suma de Ángulos Internos
En todo triángulo se cumple que la suma de los ángulos internos es igual a 180°, al ser tres ángulos tenemos:
a + b + c = 180 °
Ejemplo 1:
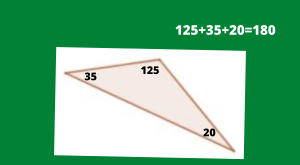
En este ejemplo se puede apreciar que la suma de sus ángulos interiores es 180º. Un ejemplo es el triángulo de la siguiente figura, donde consta la suma mencionada y su resultado:
Propiedad 02: Suma de Ángulos Externos
La suma de las medidas de los ángulos externos de un triángulo da como resultado a 360°.
a + b + c = 360 °
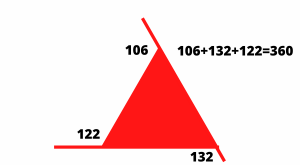
A continuación a través de la siguiente gráfica mostramos el cumplimiento de la segunda propiedad de triángulos:
Propiedad 3: Relación entre un ángulo Externo y dos Internos
La suma de dos ángulos internos de un triángulo es igual al ángulo externo no adyacente a ellos.
x = a + b
Ejemplo 3:
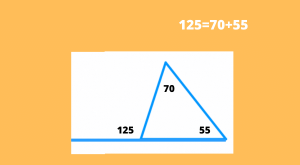
Cada ángulo exterior de un triángulo es igual a la suma de los dos ángulos interiores opuestos del triangulo no adyacentes. La propiedad tercera de triángulos se puede apreciar en la siguiente gráfica:
Clasificación de un triángulo
Según la medición del ángulo, los triángulos se clasifican en:
- Agudo En Ángulo
- Rectángulo
- Anguloso obtuso
- Triángulo escaleno
- Isósceles
- Triángulo equilátero
Triángulo de ángulo agudo
Un triángulo que tiene los tres ángulos inferiores a 90 es un triángulo de ángulo agudo.
- Entonces, todos los ángulos de un triángulo de ángulo agudo se llaman ángulos agudos
Triángulo Recto
Un triángulo que tiene un ángulo que mide exactamente 90 es un triángulo rectángulo.
- Los otros dos ángulos de un triángulo rectángulo son ángulos agudos.
- El lado opuesto al ángulo recto es el lado más grande del triángulo y se llama hipotenusa.
En un triángulo rectángulo, la suma de los cuadrados de los lados perpendiculares es igual al cuadrado de la hipotenusa.
Por ejemplo, considerando el triángulo rectángulo ACB anterior, podemos decir:
(AC) ^ 2 + (CB) ^ 2 = (AB) ^ 2
Esto se conoce como teorema de Pitágoras. Podemos decir que si un triángulo satisface la condición de Pitágoras, entonces es un triángulo rectángulo.
Como ejemplos de triángulos rectos se pueden mencionar:
Ejemplo 1: Triángulo 45-45-90
En este triangulo
- Dos ángulos miden 45, y el tercer ángulo es un ángulo recto.
- Los lados de este triángulo estarán en la relación – 1: 1: √2 respectivamente.
- Esto también se llama triángulo isósceles en ángulo recto ya que dos ángulos son iguales.
Ejemplo 2: Triángulo 30-60-90
En este triangulo
- Este es un triángulo rectángulo, ya que un ángulo = 90
- Los ángulos de este triángulo están en la relación: 1: 2: 3 y
- Los lados opuestos a estos ángulos estarán en la relación – 1: √3: 2 respectivamente
- Este es un triángulo rectángulo escaleno ya que los tres ángulos son diferentes.
Triángulo de ángulo obtuso / oblicuo
Un triángulo que tiene un ángulo que mide más de 90 es un triángulo de ángulo obtuso.
Triángulo escaleno
Un triángulo que tiene los tres lados de diferentes longitudes es un triángulo escaleno.
Como los tres lados son de diferentes longitudes, los tres ángulos también serán diferentes.
Triángulo isósceles
Un triángulo que tiene dos lados de la misma longitud y el tercer lado de una longitud diferente es un triángulo isósceles.
- Los ángulos opuestos a los lados iguales miden lo mismo.
Triángulo equilátero
Un triángulo que tiene los tres lados de la misma longitud es un triángulo equilátero.
- Como los tres lados tienen la misma longitud, los tres ángulos también serán iguales.
- Cada ángulo interior de un triángulo equilátero = 60