Las geometria figuras son los elementos geométricos muy importantes dentro de las ramas matemáticas que se pueden definir como una serie de puntos que se (conjunto de puntos o elementos) encuentran en un mismo lugar. Las figuras geométricas pueden tener variadas dimensiones, lo cual nos sirve para clasificarlas y organizar su entendimiento.
Las geometria figuras principales que conocemos son Triángulos, Cuadrados, Rombos, Circunferencias, Elipses, Pirámides y pentágonos. Los dos aspectos más importantes dentro de las figuras geométricas son el área y el perímetro:
Area: Es definida como la superficie de una figura o el espacio que se encuentra en la parte interior de la figura.
Perímetro: El perímetro es la distancia alrededor de una figura de dos dimensiones, o la medición de la distancia en torno a algo; la longitud de la frontera. Es la medida del contorno de la superficie de una determinada figura o también conocida como la suma de los lados de la figura.
A continuación se pueden ver tres figuras geometricas para resolver:
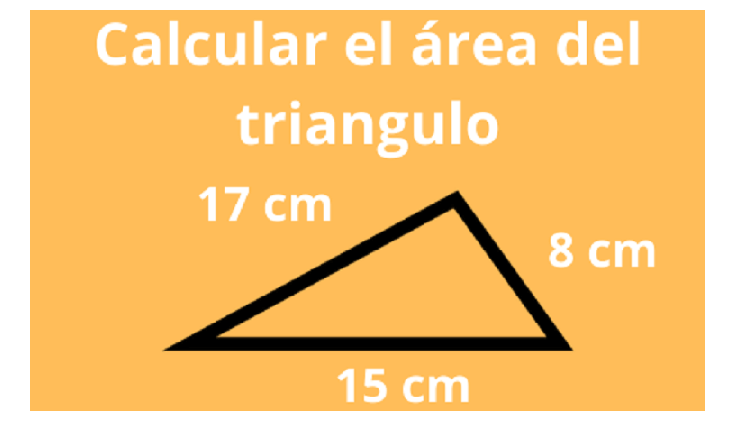
Ejercicio 1 Calcular el área del triangulo: geometria figuras

Para calcular el área de un triangulo, primero se deberá calcular el perímetro que es la suma de sus lados, con lo cual se obtendrá:
Perimetro = a+b+c = 17 + 8 + 15
A partir del perímetro, se determina el semiperimetro dividiendo el mismo entre dos por lo que tendremos:
S= Semiperimetro = Perimetro/2= 40/2=20
Con el dato del semi perimetro, ahora si se puede calcular el área en base a la siguiente fórmula:
Area = A = Raíz{[s(s-a)(s-b)(s-c)]}
Reemplazando los valores del semiperimetro y de los lados del ytriangulo tenemos:
Area = A = Raíz{[20m(20m-17m)(20m-8m)(20m-15m)]}
Area = A = Raíz{[20m(3m)(12m)(5m)]}
Area = A = Raíz(3600)
Por lo que el área del triangulo sera de Area = A = 60
HAGA CLICK PARA VER 100 EJERCICIOS DE ALGEBRA
Ejercicio 2 Calcular el área del triangulo: geometria figuras
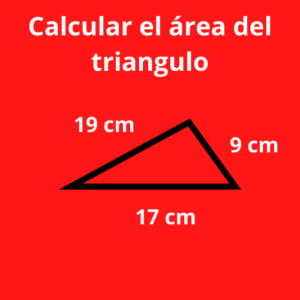
Para calcular el área de un triangulo, primero se deberá calcular el perímetro que es la suma de sus lados, con lo cual se obtendrá:
Perimetro = a+b+c = 19 + 9 + 17
A partir del perímetro, se determina el semiperimetro dividiendo el mismo entre dos por lo que tendremos:
S= Semiperimetro = Perimetro/2 = 45/2 = 22,5
Con el dato del semi perimetro, ahora si se puede calcular el área en base a la siguiente fórmula:
Area = A = Raíz{[s(s-a)(s-b)(s-c)]}
Reemplazando los valores del semiperimetro y de los lados del ytriangulo tenemos:
Area = A = Raíz{[22,5(22,5-19)(22,5-9)(22,5-17)]}
Area = A = Raíz{[22,5m(3,5m)(13,5m)(5,5m)]}
Area = A = Raíz(5847)
Por lo que el área del triangulo sera de Area = A = 76,47
HAGA CLICK PARA VER EJERCICIOS PARA FACTORIZAR
Ejercicio 3 Calcular el área del triangulo:

Para calcular el área de un triangulo, primero se deberá calcular el perímetro que es la suma de sus lados, con lo cual se obtendrá:
Perimetro = a+b+c = 21 + 10 +19
A partir del perímetro, se determina el semiperimetro dividiendo el mismo entre dos por lo que tendremos:
S= Semiperimetro = Perimetro/2= 50/2=25
Con el dato del semi perimetro, ahora si se puede calcular el área en base a la siguiente fórmula:
Area = A = Raíz{[s(s-a)(s-b)(s-c)]}
Reemplazando los valores del semiperimetro y de los lados del triangulo tenemos:
Area = A = Raíz{[25m(25m-21m)(25m-10m)(25m-19m)]}
Area = A = Raíz{[25m(4m)(15m)(6m)]}
Area = A = Raíz(9000)
Por lo que el área del triangulo sera de Area = A = 94,86