Entendemos por figuras geométricas a las superficies planas delimitadas por líneas que pueden ser curvas o rectas. Entre la figura geométricas más conocida se encuentra el triángulo.
El triángulo recibe ese nombre debido a que tiene tres lados y este resulta de unir tres puntos y donde se pueden ver tres líneas en forma de recta. Donde se cruzan dos líneas se llaman vértices.
Existen diferentes tipos de triángulos que son es el triángulo rectángulo; el cual está compuesto por dos catetos y una hipotenusa, el triángulo equilátero donde lados son iguales, el Isósceles dos lados iguales y uno distinto, y finalmente en el escaleno que son los, tres lados distintos.
A continuación se pueden ver tres figuras geométricas de triángulos para resolver:
Ejercicio 1: Calcular la altura de las figuras del triangulo
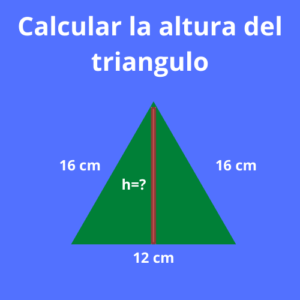
Para conocer la altura dividiremos el triángulo en dos pequeños triángulos rectángulos. Como la base del triángulo grande es de 12 cm al dividirlo en dos triángulos pequeños tendremos una base de 6 cm; que también es conocido como cateto. La hipotenusa es de 16 cm por lo que como datos tendremos lo siguiente:
Cateto1= 6 cm
Hipotenusa = 16 cm
El teorema de Pitágoras dice que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de sus catetos. Por tanto, en el siguiente triangulo tendremos:
(Hipotenusa)^2 = (Cateto1)^2 + (Cateto2)^2
(16)^2 = (6)^2 + (Cateto2)^2
256 = 36 + (Cateto2)^2
220 = (Cateto2)^2
(Cateto2)^2= 220 cm
Por lo que el segundo cateto, es decir la altura será Cateto2= 14,83 cm
HAGA CLICK PARA VER SISTEMA DE ECUACIONES
Ejercicio 2: Calcular la altura de las figuras del triangulo
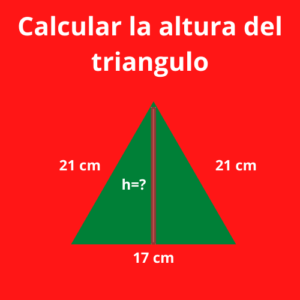
Para conocer la altura dividiremos el triángulo en dos pequeños triángulos rectángulos. Como la base del triángulo grande es de 17 cm al dividirlo en dos triángulos pequeños tendremos una base de 8,5 cm; que también es conocido como cateto. La hipotenusa es de 16 cm por lo que como datos tendremos lo siguiente:
Cateto1= 8,5 cm
Hipotenusa = 21 cm
El teorema de Pitágoras dice que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de sus catetos. Por tanto, en el siguiente triangulo tendremos:
(Hipotenusa)^2 = (Cateto1)^2 + (Cateto2)^2
(21)^2 = (8,5)^2 + (Cateto2)^2
441 = 72,25 + (Cateto2)^2
368,75 = (Cateto2)^2
(Cateto2)^2= 368,75 cm
Por lo que el segundo cateto, es decir la altura será Cateto2= 19,2 cm
HAGA CLICK PARA VER LIBROS DE MATEMATICAS
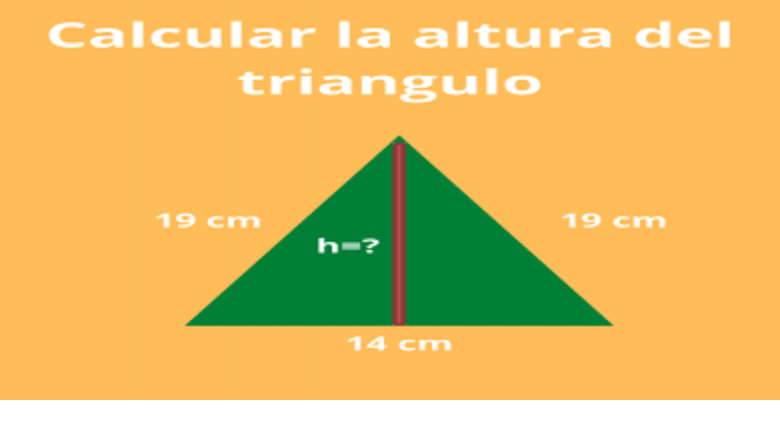
Ejercicio 3: Calcular la altura del triangulo

Para conocer la altura dividiremos el triángulo en dos pequeños triángulos rectángulos. Como la base del triángulo grande es de 14 cm al dividirlo en dos triángulos pequeños tendremos una base de 7 cm; que también es conocido como cateto. La hipotenusa es de 16 cm por lo que como datos tendremos lo siguiente:
Cateto1= 7 cm
Hipotenusa = 19 cm
El teorema de Pitágoras dice que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de sus catetos. Por tanto, en el siguiente triangulo tendremos:
(Hipotenusa)^2 = (Cateto1)^2 + (Cateto2)^2
(19)^2 = (7)^2 + (Cateto2)^2
361 = 49 + (Cateto2)^2
312 = (Cateto2)^2
(Cateto2)^2= 312 cm
Por lo que el segundo cateto, es decir la altura será Cateto2= 17,66 cm