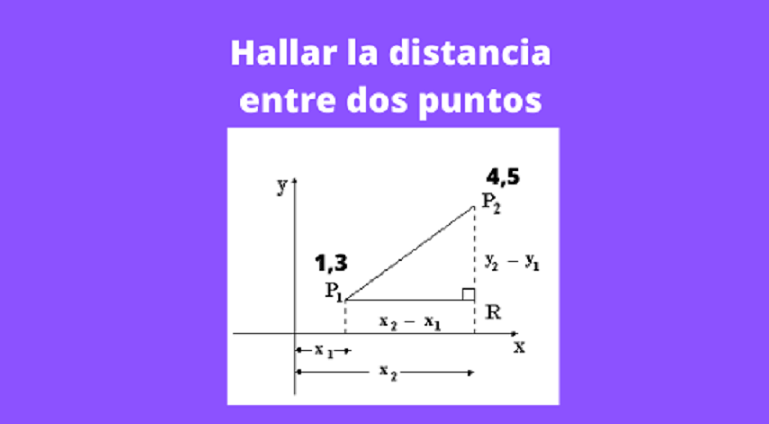
En el presente artículo explicamos como calcular la distancia entre dos puntos dadas las coordenadas de dos puntos, P1 y P2. Se usa una fórmula de distancia entre estos dos puntos. Un ejemplo muestra cómo usar la fórmula para determinar la distancia de dos puntos dadas sus coordenadas.
Se debe calcular entre cada par de puntos dados usando la fórmula de distancia.
Por haberlo estudiado, sabemos que el Plano cartesiano se usa como un sistema de referencia para localizar puntos en un plano.
Los puntos se encuentran ubicados sobre el eje x (de las abscisas) y en el eje y (de las ordenadas), la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas. Ahora, si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:
Distancia = d= Raíz {[(X2-X1)^2]+[ (Y2-Y1)^2]}
A continuación se pueden ver tres ejercicios relacionados con la distancia entre dos puntos:
Ejercicio 1: Determine la distancia entre los siguientes puntos P1(1,3) y P2(4,5)
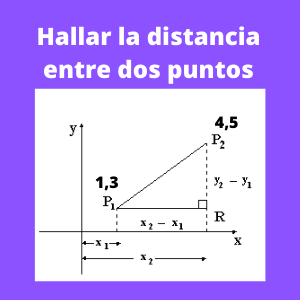
La fórmula de la distancia entre 2 puntos es la siguiente:
Distancia = d= Raíz {[(X2-X1)^2]+[ (Y2-Y1)^2]}
Se quiere calcular la distancia entre los siguientes puntos P1(1,3) y P2(4,5), por lo que reemplazando en la fórmula expuesta se tiene:
Distancia = d= Raíz {[(4-1)^2]+[ (5-3)^2]}
Distancia = d= Raíz {[3^2]+[2^2]}
Se eleva al cuadrado la diferencia de datos sobre el eje x (de las abscisas) y eje y (de las ordenadas), obteniendo de esta manera los siguientes resultados:
Distancia = d= Raíz {9+4}
Distancia = d= Raíz {13}
HAGA CLICK PARA VER EJERCICIOS DE SISTEMAS DE ECUACIONES
Ejercicio 2: Determine la distancia entre P1(2,2) y P2(5,6)
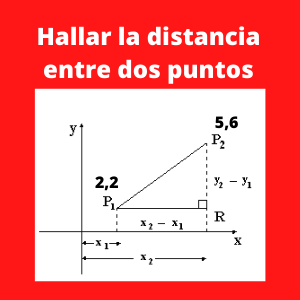
La fórmula de la distancia entre puntos es la siguiente:
Distancia = d= Raíz {[(X2-X1)^2]+[ (Y2-Y1)^2]}
Se quiere calcular la distancia entre los siguientes puntos P1(2,2) y P2(5,6), por lo que reemplazando en la fórmula expuesta se tiene:
Distancia = d= Raíz {[(5-2)^2]+[ (6-2)^2]}
Distancia = d= Raíz {[3^2]+[4^2]}
Se eleva al cuadrado la diferencia de datos sobre el eje x (de las abscisas) y eje y (de las ordenadas), obteniendo de esta manera los siguientes resultados:
Distancia = d= Raíz {9+16}
Distancia = d= Raíz {20}
HAGA CLICK PARA DESCARGAR LIBROS DE MATEMATICAS
Ejercicio 3: Determine la distancia entre dos puntos P1(3,3) y P2(7,5)
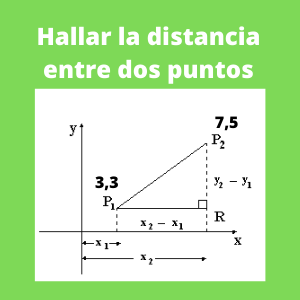
La fórmula de la distancia entre 2 puntos es la siguiente:
Distancia = d= Raíz {[(X2-X1)^2]+[ (Y2-Y1)^2]}
Se quiere calcular la distancia entre los siguientes puntos P1(2,2) y P2(5,6), por lo que reemplazando en la fórmula expuesta se tiene:
Distancia = d= Raíz {[(7-3)^2]+[ (5-3)^2]}
Distancia = d= Raíz {[4^2]+[2^2]}
Se eleva al cuadrado la diferencia de datos sobre el eje x (de las abscisas) y eje y (de las ordenadas), obteniendo de esta manera los siguientes resultados:
Distancia = d= Raíz {16+4}
Distancia = d= Raíz {20}