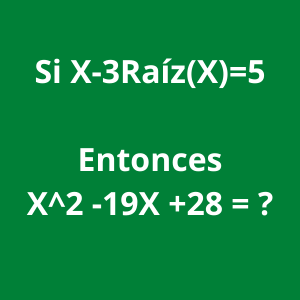Para poder resolver ejercicios de una potencia de potencia lo que se realiza es multiplicar los exponentes de dicha potencia y obtener el resultado de la misma.
La potencia consta de dos elementos: la base y los exponentes. Equivale a multiplicar la base el número de veces que dice el exponente. En general, es igual al producto de las potencias de los factores. Como ejemplos se puede mencionar:
Ejemplo: 2^4, significa que la base es 2 y el exponente es 4 por lo que multiplicaremos 4 veces el 2; es decir 2*2*2*2=16.
Ejemplo: 3^5, significa que la base es 3 y el exponente es 5 por lo que multiplicaremos 5 veces el 3; es decir 3*3*3*3*3=243.
A continuación se pueden observar los tres mejores ejercicios de potencia de potencia resueltos:
Ejercicio 1 Potencias:
Si X-3Raíz(X)=5
Entonces
X^2 -19X +28 = ?
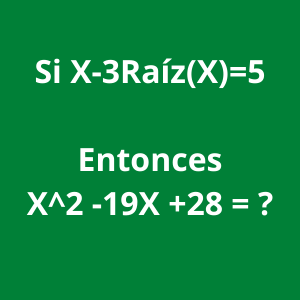
De la presente ecuación X-3Raíz(X)=5, buscaremos eliminar la raíz para lo cual pondremos en el lado derecho los términos que tienen raíz y en el lado izquierdo los que no tienen quedando X-5=3Raíz(X). Ahora para eliminar la raíz elevamos la ecuación al cuadrado de esta manera (X-5)^2=(3Raíz(X))^2 dándonos un resultado (X-5)^2=9X. Posteriormente desarrollamos el término cuadrático dando como resultado X^2-10X+25=9X y hacemos operaciones para finalmente tener este valor X^2-19X+25=0.
Ahora buscaremos que la ecuación tenga esta forma X^2 -19X +28 = ?, por lo que sumaremos a ambos lados 3 dando X^2-19X+25+3=3; por lo que finalmente el valor buscado es el siguiente:
X^2-19X+28=3
HACE CLICK PARA VER TODO TIPO DE EJERCICIOS DE MATEMATICAS
Ejercicio 2: (X+2)^3=X^3+6X^2

Debemos tener en cuenta que los productos notables nos dicen que:
(a+b)^3=a^3+3(a^2)*b+ 3a(b^2)+b^3
Por lo que al desarrollar el ejercicio (X+2)^3=X^3+6X^2 obtendremos lo siguiente X^3+(3X^2)*2+ 3X(2^2)+2^3=X^3+6X^2. Realizando las multiplicaciones correspondientes tendremos la siguiente ecuación X^3+6X^2+ 12X+8=X^3+6X^2. Finalmente desarrollando encontraremos el valor de X que es de:
12X+8=0
X=-8/12
X=-2/3
HACE CLICK PARA VER EJERCICIOS DE ORDEN DE OPERACIONES
Ejercicio 3 Potencia de potencia: {[(2^-4)^4]*(2^17)}^4

Para poder resolver la siguiente ecuación {[(2^-4)^4]*(2^17)}^4 primero veremos que la base de cada término tenga un solo exponente por lo que quedará {(2^-16)*(2^17)}^4. Multiplicando dos valores que tienen la misma base y diferentes exponentes obtendremos {2^1}^4. Por lo que el resultado final será de 2^4 es decir 16.