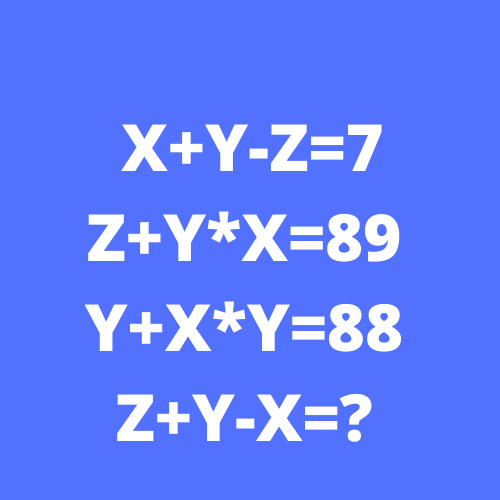¿Que son las ecuaciones? Los sistemas de ecuaciones lineales permiten resolver problemas de ingeniería, física, química, etc. Se trata a partir de varias ecuaciones lineales se podrá encontrar las incógnitas de las variables. Para poder resolver un sistema de ecuaciones lineales se deben seguir los siguientes pasos:
- Se despeja una incógnita en una ecuación.
- Sustituye la expresión de esta incógnita en la otra ecuación, obteniendo un ecuación con una sola incógnita.
- Resuelve la ecuación.
- El valor obtenido se sustituye en la ecuación en la que aparecía la incógnita despejada.
Existen tres tipos de resultados en un sistema de ecuaciones, los cuales son:
- Tiene una sola solución.
- Indeterminado tiene infinitas soluciones.
- No tiene solución.
A continuación se pueden apreciar 3 ejercicios para entender que son las ecuaciones:
Ejercicio 1: Sí X+Y-Z=7, Z+Y*X=89 y Y+X*Y=88. Determinar Z+Y-X=?
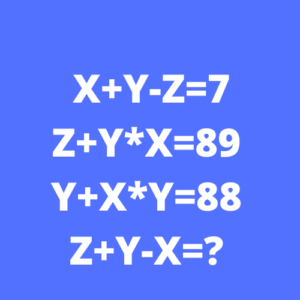
El problema se plantea con tres ecuaciones con tres incógnitas:
X+Y-Z=7
Z+Y*X=89
Y+X*Y=88
Se debe calcular el valor de X,Y y Z inicialmente para poder resolver el problema, lo cual se realizará de la siguiente manera:
Entre la ecuación 1 y la ecuación 2 se buscará eliminar el valor de Z
X+Y-Z=7
Z+Y*X=89
Sumando las mismas se obtiene
X+Y+Y*X=96
Con esto podremos tener dos ecuaciones con dos incógnitas las cuales son las siguientes:
X+Y+Y*X=96
Y+X*Y=88
Restando la segunda de la primera ecuación se llegará a obtener:
X=8
Ahora volvemos a ver las dos ecuaciones anteriormente descrita, pero reemplazando X con lo cual tendremos:
8+Y-Z=7
Z+8Y=89
Sumando ambas ecuaciones llegamos a obtener:
8+9Y=96
9Y=88
Y=88/9
Finamente despejamos Z en la primera ecuación con lo cual tendremos:
X+Y-Z=7
Z=X+Y-7
Z=8+(88/9)-7
Z=97/9
Ahora que encontramos los valores de X,Y y Z resolveremos la ecuación de Z+Y-X=? dando como resultado Z+Y-X=97/9 + 88/9 – 72/9 = 113/9
Ejercicio 2 Que son las ecuaciones: Sí X+Y-Z=0, Z+Y*X=5 y Y+X*Y=4. Determinar Z+Y-X=?
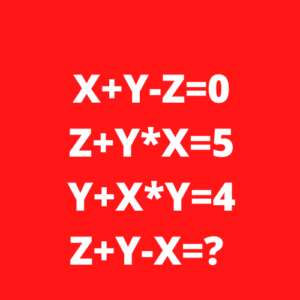
El problema se plantea con tres ecuaciones con tres incógnitas:
X+Y-Z=0
Z+Y*X=5
Y+X*Y=4
Se debe calcular el valor de X,Y y Z inicialmente para poder resolver el problema, lo cual se realizará de la siguiente manera:
Entre la ecuación 1 y la ecuación 2 se buscará eliminar el valor de Z
X+Y-Z=0
Z+Y*X=5
Sumando las mismas se obtiene
X+Y+Y*X=5
Con esto podremos tener dos ecuaciones con dos incógnitas las cuales son las siguientes:
X+Y+Y*X=5
Y+X*Y=4
Restando la segunda de la primera ecuación se llegará a obtener:
X=1
Ahora volvemos a ver las dos ecuaciones anteriormente descrita, pero reemplazando X con lo cual tendremos:
1+Y-Z=0
Z+Y=5
Sumando ambas llegamos a obtener:
1+2Y=5
2Y=4
Y=2
Finamente despejamos Z en la primer ecuación con lo cual tendremos:
X+Y-Z=0
Z=X+Y
Z=1+2
Z=3
Ahora que encontramos los valores de X,Y y Z resolveremos la ecuación de Z+Y-X=? dando como resultado Z+Y-X=3 + 2 – 1 = 4
Ejercicio 3: Sí X+Y-Z=2, Z+Y*X=17 y Y+X*Y=16. Determinar Z+Y-X=?
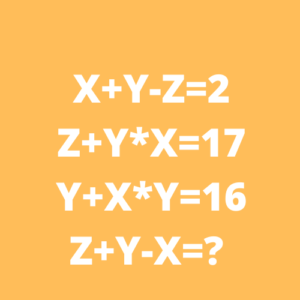
El problema se plantea con tres ecuaciones con tres incógnitas:
X+Y-Z=2
Z+Y*X=17
Y+X*Y=16
Se debe calcular el valor de X,Y y Z inicialmente para poder resolver el problema, lo cual se realizará de la siguiente manera:
Entre la ecuación 1 y la ecuación 2 se buscará eliminar el valor de Z
X+Y-Z=2
Z+Y*X=17
Sumando las mismas se obtiene
X+Y+Y*X=19
Con esto podremos tener dos ecuaciones con dos incógnitas las cuales son las siguientes:
X+Y+Y*X=19
Y+X*Y=16
Restando la segunda de la primera ecuación se llegará a obtener:
X=3
Ahora volvemos a ver las dos ecuaciones anteriormente descrita, pero reemplazando X con lo cual tendremos:
3+Y-Z=2
Z+3Y=17
Sumando ambas llegamos a obtener:
3+4Y=19
4Y=16
Y=4
Finamente despejamos Z en la primer ecuación con lo cual tendremos:
X+Y-Z=2
Z=X+Y-2
Z=3+4-2
Z=5
Ahora que encontramos los valores de X,Y y Z resolveremos la ecuación de Z+Y-X=? dando como resultado Z+Y-X=5 + 4 – 3 = 6