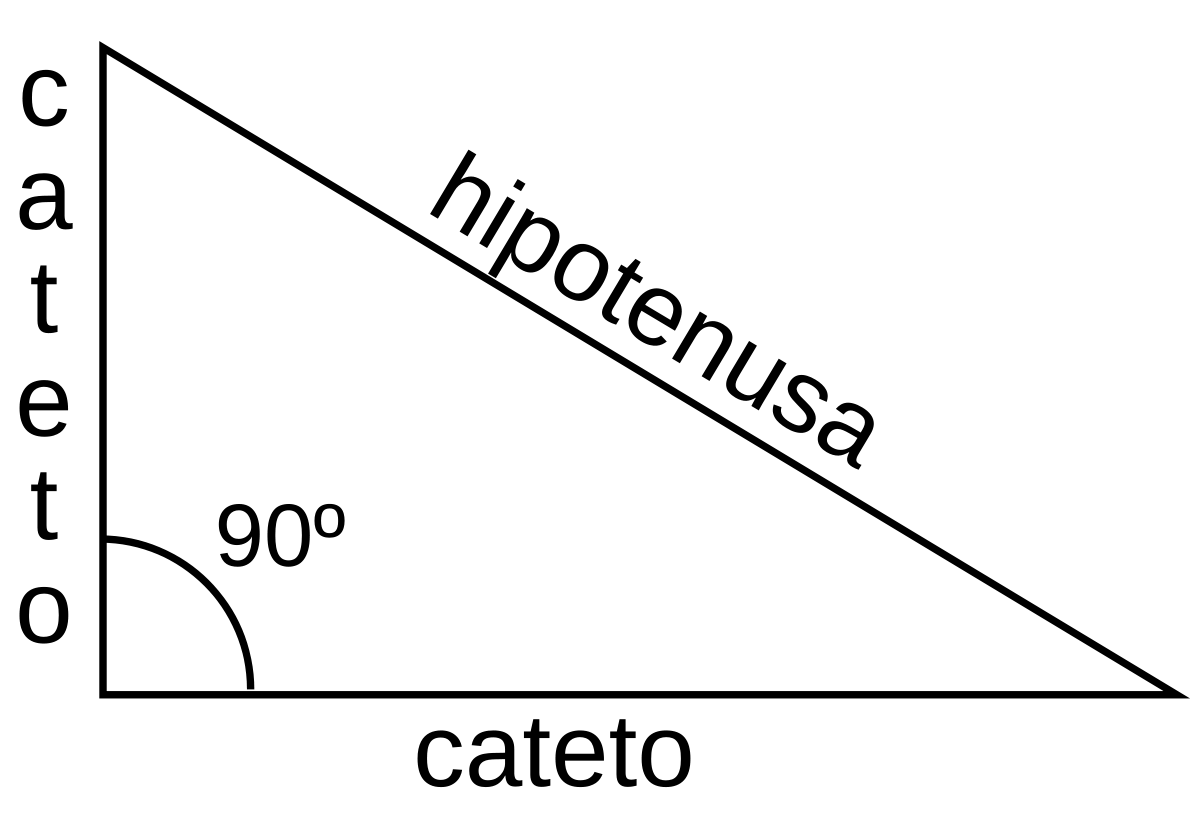
La hipotenusa es el lado de un triángulo rectángulo que está al frente del ángulo recto o de 90º. De esta forma, se trata del lado de más grande longitud de la figura.
La hipotenusa es entonces el lado de un triángulo rectángulo que tiene más grande medida que los demás 2 lados, a los que se le llama catetos.
Debemos rememorar que un triángulo rectángulo es ese que tiene un ángulo recto y otros 2 que son agudos, puesto que la suma de los ángulos interiores de cualquier triángulo debería ser igual a 180º.
Fórmula de la hipotenusa
Para describir la fórmula, debemos tomar en consideración que un triángulo rectángulo se cumple el teorema de Pitágoras. Este sugiere que la hipotenusa al cuadrado es igual a la suma de todos los catetos al cuadrado.
O sea, matemáticamente la hipotenusa se puede conceptualizar por medio de la siguiente fórmula, donde la hipotenusa es AC y los catetos son AB y BC.
AC^2=AB^2+BC^2
Triángulo rectángulo
Otra forma de explicarlo es que la suma de las longitudes de las proyecciones ortogonales de ambos catetos da como consecuencia la longitud de la hipotenusa. Viendo la imagen inferior, donde el segmento BE es perpendicular a AC, la hipotenusa podría ser:
AC= AE +EC
Otro cosa a tener en cuenta es que la hipotenusa es equivalente al diámetro de la circunferencia a la cual el triángulo rectángulo está inscrito.
Cabe explicar además que el diámetro es el segmento de une 2 punto opuestos de la circunferencia pasando por su centro.
Ejemplo
Supongamos que poseemos un cuadrado cuyos lados miden 9 metros. ¿Cuál va a ser la longitud de su diagonal? Aquí debemos rememorar que un cuadrado tiene no solo todos sus lados equivalentes, sino que sus ángulos interiores además miden lo mismo y son rectos.
De aquel modo, si trazamos una diagonal nos quedan 2 triángulos rectángulos equivalentes donde la diagonal es la hipotenusa.
Por consiguiente, siguiendo el teorema de Pitágoras, tenemos la posibilidad de encontrar la longitud de la diagonal (DB):
DB^2=AB^2+AD^2
DB^2=9^2+9^2
DB^2=162= Raiz(162) m