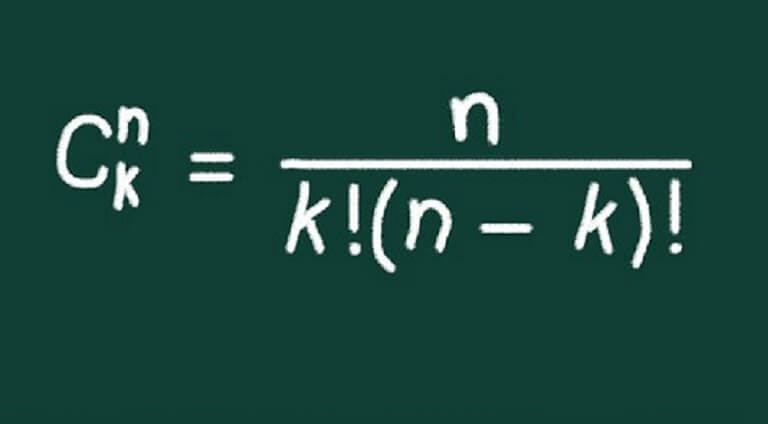Ejercicios de Combinatoria

Los ejercicios de combinatoria estudian la cantidad de maneras diferentes en las que se pueden considerar conjuntos que se forman partiendo de elementos de un conjunto inicial. La Combinatoria es la parte de Matemáticas que se encarga de crear grupos de datos, objetos y llevar a cabo los cálculos necesarios.

Un problema combinatorio suele consistir en establecer una regla acerca de la forma en la cual se deben dar las llamadas agrupaciones y determinar cuántas de ellas  satisfacen la regla. Se deben tener en cuenta las combinaciones, las variaciones y las permutaciones. En los problemas combinatorios hay varios conceptos claves que debemos distinguir:

1 Población

Es el conjunto de elementos que estamos estudiando. Denominaremos m al número de elementos de este conjunto.

2 Muestra

Es un subconjunto de la población. Denominaremos n al número de elementos que componen la muestra. Los diferentes tipos de muestra tienen dos aspectos:

Orden: Los elementos de la muestra aparezcan ordenados o no.

Repetición: La posibilidad de repetición o no de los elementos.

Variaciones  y  Combinaciones.

Ejercicios de Variaciones

Llamamos variaciones a los distintos grupos de elementos que podemos formar tomados de n en n de un total de m elementos.

1 ¿Cuántos grupos de 2 cifras (n) podemos formar con las cifras 1,2,3 (m)?

Los grupos de 2 elementos son: 12, 13, 21, 23, 31 y 32

Vemos que con 3 cifras podemos formar 6 números diferentes de dos.

V = n!/(n-r)!

V = 3!/(2-1)! = 6

Ejercicios de Combinatoria

2 En una clase de danza hay 4 alumnos y se quiere formar un comité de 3 personas ¿De cuántas maneras distintas es posible?

Si ordenamos de diferente manera los elementos en nuestra muestra se obtiene el mismo comité.

Es decir, Ana, Rosa y Pedro forman el mismo comité que Pedro, Rosa y Ana.

¿Puede haber elementos repetidos en la muestra?

No, puede haber elementos repetidos en la muestra.

A partir de las siguientes fórmulas se puede calcular:

P = n!/((n-r)!*r!)

P = 4!/((4-3)!)/3!) = 4!/3! = 4

A continuación se pueden ver ejercicios de combinatoria:

HAGA CLICK EN LAS IMAGENES