El teorema del residuo es el efecto directo del Teorema Integral de Cuchy, siendo una sección bastante fundamental en la teoría matemática del estudio complejo.
Aplicación del teorema del residuo para polinomios
La separación de polinomios está entre una enorme proporción de operaciones algebraicas, y entre ellas tenemos la posibilidad de encontrarnos con la operación especifica de dividir un polinomio entre un binomio.
En esta situación específica, una vez que un polinomio se divide entre un binomio, generalmente se muestra un residuo.
En el teorema del residuo está establecido que una vez que un polinomio de x, f(x) se divide entre (x – a), en donde cualquier número equivale a cualquier número real o complejo, entones el residuo es f(a).
Esto significa que para lograr hallar el residuo una vez que el polinomio se divide entre un binomio el costo de x es equivalente al costo de a, o f(x) = f(a).
De esta forma, se tiene que calcular el costo de x, el cual va a ser igual que el costo de a.
Si consideramos el polinomio x² – 8 x + 6, el cual se puede detectar como una funcionalidad polinomial f(x) = x² -8 x + 6.
Aquí se tiene que dividir el polinomio entre el binomio x – 2 para lograr descubrir el residuo.
En esta situación la división se puede hacer de la siguiente forma:
Primer Método: Division extensa
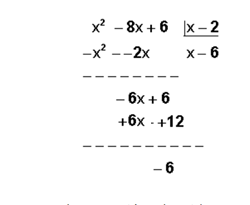
Como tenemos la posibilidad de ver en la operación, el residuo resultante es -6.
Segundo Método: División sintética
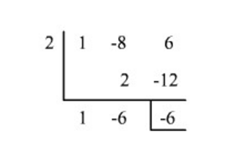
De la misma forma, el residuo es -6.
Método 3: Uso del teorema del residuo
f(x) = x² – 8 x + 6 dividido entre x – 2,
En esta situación, para lograr calcular el costo de x, hacemos x – 2 = 0
x = 2
Gracias al teorema tenemos la posibilidad de saber que x = a, y de esta forma tenemos la posibilidad de reemplazarlo en el polinomio al dividir:
2 ² – 8 (2) + 6 y se tiene que solucionar 4 – 16 + 6 = -6
Como vemos en este tercer procedimiento, el residuo obtenido además es de -6, el mismo que obtuvimos con ambos procedimientos anteriores al dividir un polinomio entre un binomio.

