Los conjuntos matematicos se definen a una cantidad de elementos que tienen características parecidas. Existen conjuntos en números, letras, figuras, etc. En el caso de las matemáticas varios elementos formaran un conjunto. Los conjuntos matematicos pueden tener un número finito o infinito de elementos. Los conjuntos se escriben con letras mayúsculas y los elementos con minúsculas. Dos conjuntos se consideran si sus elementos son iguales.
Un conjunto está definido por los elementos que lo comprenden; es decir diferentes elementos diferentes conjuntos. AS continuación se puede ver cuatro ejercicios resueltos de conjuntos matemáticos:
Ejercicio 1 conjuntos matematicos: Determinar a cuantos no les gusta ni las matemáticas ni la física a través de conjuntos.

En un aula de clase hay 34 alumnos de los a cuales a 21 les gusta las matemáticas, a 18 física y a 10 les gusta ambas materias. ¿A cuántos no les gusta ninguna de las dos materias?
Primeramente se colocara un nombre a cada una de las variables, que es como sigue:
M = Alumnos que les gusta sólo las Matemáticas = ¿?
F = Alumnos que les gusta sólo la Física = ¿?
A = Alumnos que les gusta ambas materias = 10
N= Alumnos que no les interesa ninguna de las dos materias = ¿?
M2 = Alumnos que les gusta las Matemáticas = 21
F2 = Alumnos que les gusta la Física = 18
TA= Total alumnos = 34
Del problema se puede deducir que los Alumnos que les gusta sólo las matemáticas es igual a los alumnos que les gustan ambas materias menos los alumnos que les gusta las matemáticas, tal como se puede ver en la siguiente ecuación:
M=M2-A
Reemplazando tendremos:
M=21-10=11
Del problema se puede deducir que los Alumnos que les gusta sólo la física es igual a los alumnos que les gustan ambas materias menos los alumnos que les gusta la física, tal como se puede ver en la siguiente ecuación:
F=F2-A
Reemplazando tendremos:
F=18-10=8
Por lo tanto los Alumnos que les gusta sólo las matemática más los Alumnos que les gusta ambas materias más Alumnos que les gusta sólo la física más los Alumnos que no les interesa ninguna de las dos materias da como resultado el total de alumnos, tal como se puede ver en la siguiente ecuación:
M+F+A+N=34
11+8+10+N=34
Por lo que el resultado, N=5
HAGA CLICK PARA VER TODO TIPO DE EJERCICIOS DE MATEMATICAS
Ejercicio 2 conjuntos matematicos: Determinar el valor de X

En un aula hay 60 alumnos de los cuales a 7 no les gusta ni geometría ni aritmética y a 35 les gusta solo aritmética ¿A cuántos les gusta geometría si a los que les gusta ambos cursos son 10?
Primeramente se colocara un nombre a cada una de las variables a partir de la presente gráfica, que es como sigue:
G = Alumnos que les gusta sólo las Geometría = X
A = Alumnos que les gusta sólo la Aritmética = 35
AM = Alumnos que les gusta ambas materias = 10
N= Alumnos que no les interesa ninguna de las dos materias = 7
G2 = Alumnos que les gusta las Geometría = X+10
A2 = Alumnos que les gusta la Aritmética = 35+10
TA= Total alumnos = 60
De la gráfica se puede deducir que los Alumnos que les gusta sólo las Geometría más los Alumnos que les gusta ambas materias más Alumnos que les gusta sólo la Aritmética más los Alumnos que no les interesa ninguna de las dos materias da como resultado el total de alumnos, tal como se puede ver en la siguiente ecuación:
X+10+35+7=60
Por lo que el resultado, X=8
HAGA CLICK PARA VER EJERCICIOS MATEMATICOS DE UNIDADES DE MEDIDA
Ejercicio 3: Determinar el valor de X
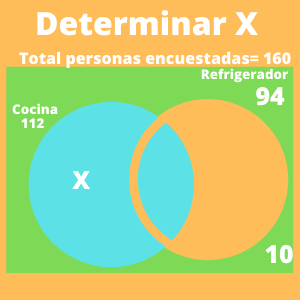
En una encuesta realizada a 160 personas 94 tienen refrigerador y 112 cocina a gas y 10 no tienen ninguno delos artefactos mencionados ¿Cuántos tienen cocina a gas solamente?
Primeramente se colocara un nombre a cada una de las variables, que es como sigue:
R = Personas que tienen sólo refrigerador = ¿?
X=C = Personas que tienen sólo cocina = ¿?
AM = Personas que tienen cocina y refrigerador = 10
N= Personas que no tienen ni cocina ni refrigerador = 10
R2 = Personas que tienen refrigerador = 94
C2 = Personas que tienen cocina = 112
TA= Total personas encuestadas = 160
De la gráfica se puede deducir que las personas que tienen sólo cocina más las personas que tienen refrigerador más las personas que tienen cocina y refrigerador da como resultado el total de personas encuestadas, tal como se puede ver en la siguiente ecuación:
X+94+10 = 160
Por lo que el resultado, X=56

