 ¿Qué es una fracción?
¿Qué es una fracción?
Una fracción es un número que tiene una longitud que no siempre será un número entero. Por lo tanto, necesitamos números que sean menores que 1: números que son partes de 1: la mitad de 1, un tercero, un cuarto, un quinto, una millonésima. El número que llamamos «un tercio», por ejemplo, se refiere a una fracción. Las fracciones son el parte de un todo. Las fracciones son números. Las fracciones tienen cantidades distintas. Tienen valor y se pueden comparar, ordenar y colocar en una recta numérica.
¿Por qué las fracciones son tan importantes en tu vida?
La pregunta en la mente de muchos estudiantes, es ¿por qué necesito fracciones? ¿Es realmente tan importante? ¿No puedo dejar esta parte y continuar con el álgebra? Solo finge que no existe.
Es triste decirlo, pero me temo que no. Las fracciones son una parte muy importante de las matemáticas. Solo piense cuántas veces al día tiene que evaluar una situación, dividir una carga de trabajo, conducir un automóvil o incluso planificar una comida.
Cuando trabajas tienes que poder dar instrucciones claras y concisas. Si planea convertirse en arquitecto, médico o cualquier puesto en un campo técnico, necesitará ciertas habilidades como fracciones para poder hacer un cálculo preciso. ¿Te imaginas si el médico o especialista cortó un centímetro demasiado y terminó matando o mutilando a su paciente? La vida de las personas depende de cálculos exactos.
Piensa en una casa sin cimientos. Se construirá sobre la arena o los escombros y cuando lleguen las tormentas, su casa estará húmeda. El piso estará embarrado y lo más probable es que en algún momento su casa se derrumbará.
Las fracciones son como esa base. Es una parte muy necesaria para mantener las paredes más adelante. Sin el conocimiento de las fracciones no podrás hacer álgebra. Cada parte de las matemáticas se basa en la parte anterior.
Las pruebas consisten en una gran parte de fracciones e incluso en la vida real las usas. Al dividir una pizza o comida en cuadrados o cuando desea dividir un espacio. Cualquiera sea la necesidad de división, sin el conocimiento de las fracciones no se podrá hacerlo.
Cuando vaya a la universidad más adelante, necesitará buenas calificaciones y, para ser honesto, sus calificaciones durante los años escolares dependen de su capacidad para hacer fracciones.
Verá, al igual que las fracciones son la base, en el futuro su casa necesitará paredes fuertes. El álgebra son esas paredes que mantendrán el techo. Entonces, si su casa de matemáticas quiere tener un buen techo más adelante, debe ser bueno en álgebra, y para ser bueno en álgebra debe ser capaz de comprender las fracciones.
Si desea sobresalir en cualquier curso de estudio que requiera matemáticas, debe tener esas cosas en una estructura sólida y buena, con una buena comprensión de cómo hacerlas.
Piensa en ti mismo como un arquitecto. Estás construyendo una casa, y lo estás haciendo una parte a la vez. Tienes que comenzar con la base. ¿Como lo haras? Al dividir la carga de trabajo y dar un paso a la vez. No avance hasta que lo entienda y pueda hacerlo con confianza.
¿Qué es una fracción común?
Un número escrito con un numerador y un denominador, en el que ambos son números naturales es una fracción común. El numerador de es 3. El denominador es 10. Se llaman los términos de la fracción.
¿Qué significan el denominador y el numerador?
El denominador nombra el número de partes iguales en las que se ha dividido el número 1. El numerador, se encuentra en la parte superior de la fracción e indica el número de partes existentes. La fracción 3/10 significa que el número 3 se ha dividido en 10 partes iguales. El número 3, en otras palabras, se ha dividido en décimas.
Como el numerador y el denominador son números naturales, el numerador tiene una relación con el denominador (tres décimas de 10) Y la fracción en sí tiene la misma proporción.
Una fracción significa una parte de un todo. En matemáticas una fracción es un número que necesitamos para medir lo que es continuo. Una fracción matemática no es simplemente una parte de un todo. Es una parte de la unidad de medida.
Ejemplo. Si el todo se divide en 5 partes iguales, y contamos 4 de ellas, ¿qué fracción es esa?
Respuesta. Esa fracción es Cuatro quintos
Por lo tanto, cada fracción es un número, una suma de fracciones unitarias. La suma y la resta, ya sea con números enteros o fracciones, se realizan con varias unidades.
¿Qué es una fracción propia?
Una fracción que es menor que 1. El numerador es más pequeño que el denominador. Dos tercios es una fracción propia. Es menos de 1.
Ejemplo. El número que escribimos como 2/3.
Ejemplo. Este número ¼ se llama «un cuarto», porque el numerador es un cuarto del denominador.
Cuando el numerador es menor que el denominador, llamamos a la expresión fracción propia. Estos son algunos ejemplos de fracciones propias.
¾, 2/3, 1/9
¿Qué es una fracción impropia?
Una fracción mayor o igual a 1. Podemos reconocer una fracción impropia cuando el numerador es mayor o igual que el denominador.
Problema. ¿Cuál de estas fracciones es menor que 1, igual a 1 o mayor que 1?
2/3, 3/2, 8/5, 8/8, 8/9, 9/9, 10/9
Una fracción impropia ocurre cuando el numerador es mayor o igual que el denominador. Estos son algunos ejemplos de fracciones impropias:
4/3, 19/7,
A continuación presentamos algunos ejemplos de fracciones propias e impropias:
| 5/8 | «Cinco octavos» |
|---|---|
| 16/3 | «Dieciséis tercios» |
| 9/2 | «Nueve mitades» |
| 27/39 | «27 sobre 39» |
| 56/1000 | «56 milésimas» |
| 5 79/100 | «5 y 79 centésimas» |
Una forma de pensar en una fracción es como una división que aún no se ha hecho. ¿Por qué incluso usamos fracciones? ¿Por qué no dividimos los dos números y usamos el decimal? En este día de calculadoras baratas, esa es una muy buena pregunta. Las fracciones se inventaron mucho antes que los números decimales, como una forma de mostrar proporciones menores o mayores que 1.
Solo para revisar, el número encima de la barra se llama numerador, y el número debajo de la barra se llama denominador.
Podemos leer esta fracción como tres cuartos, tres sobre cuatro o tres divididos por cuatro.
3/4
Cada fracción se puede convertir a un decimal dividiendo. Si usa la calculadora para dividir 3 entre 4, encontrará que es igual a 0,75.
Aquí hay algunas otras fracciones y sus equivalentes decimales. Recuerde, puede encontrar el equivalente decimal de cualquier fracción dividiendo.
½, ¼, 1/8
Aquí hay algunos términos que son muy importantes cuando se trabaja con fracciones.
Número mixto
Cuando una expresión consiste en un número entero y una fracción propia, la llamamos número mixto. Aquí hay algunos ejemplos de números mixtos:
3 1/3, 9 3/7
Podemos convertir un número mixto en una fracción impropia. Primero, multiplique el número entero por el denominador de la fracción. Luego, agregue el numerador de la fracción al producto. Finalmente, escribe la suma sobre el denominador original. En este ejemplo, dado que tres tercios es un entero, el número entero 1 es tres tercios más un tercio más, lo que equivale a cuatro tercios.
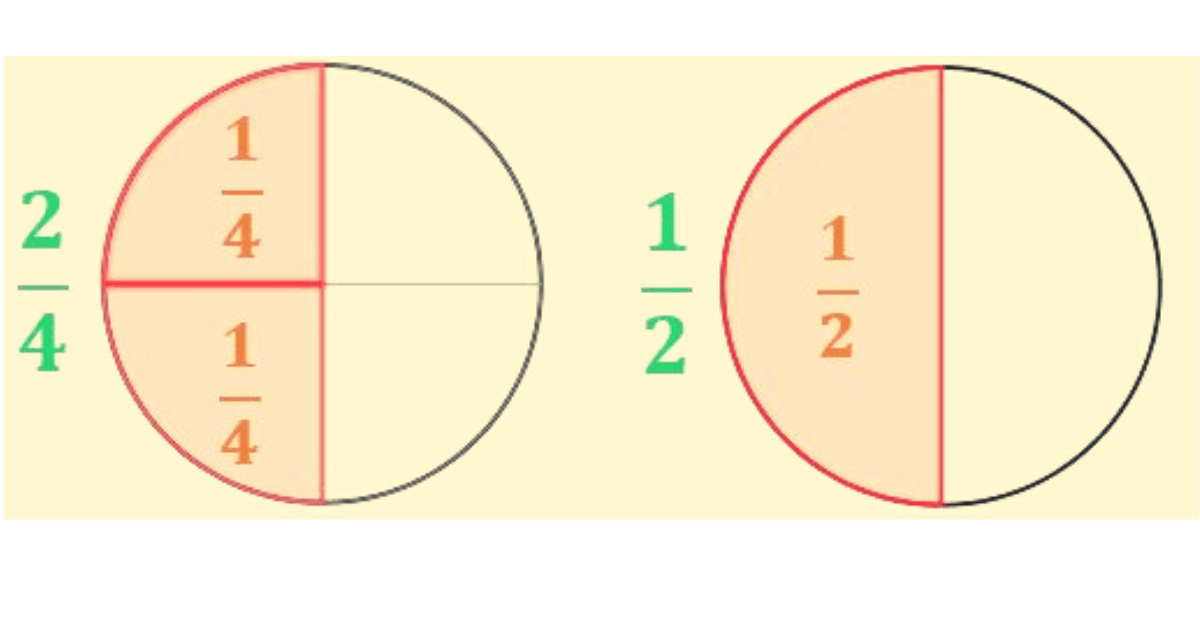
Fracciones equivalentes
Hay muchas formas de escribir una fracción de un todo. Las fracciones que representan el mismo número se llaman fracciones equivalentes. Esto es básicamente lo mismo que las proporciones iguales. Por ejemplo, ½, 2/4 y 4/8 son fracciones equivalentes. Para saber si dos fracciones son equivalentes, usa una calculadora y divide. Si la respuesta es la misma, entonces son equivalentes.