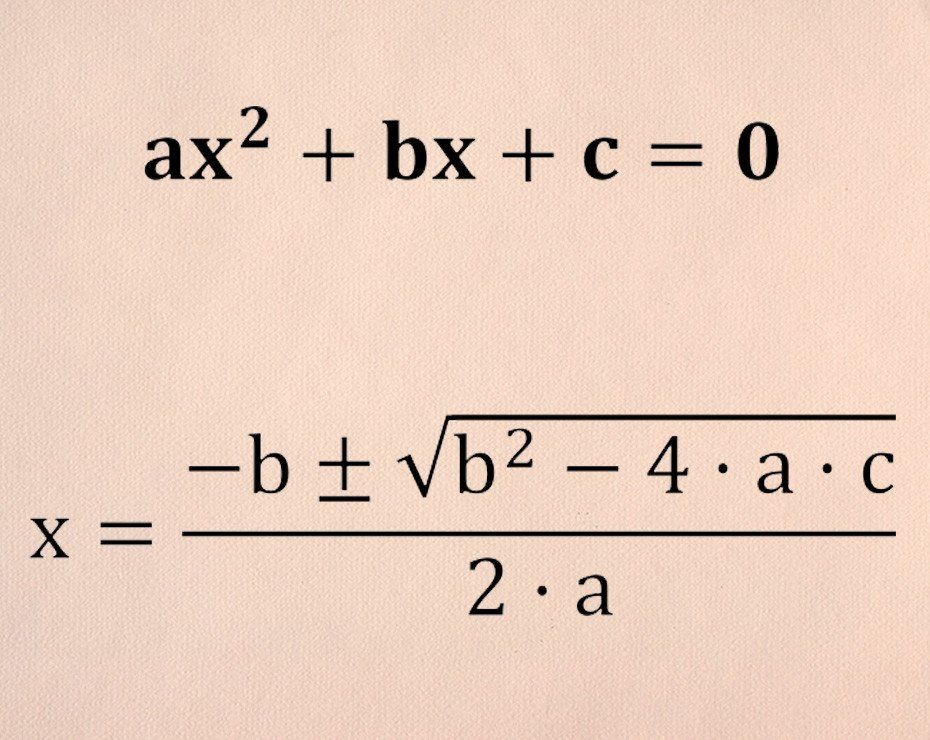En esta página resolvemos inconvenientes sobre ecuaciones de segundo nivel; donde se exige calcular las resoluciones de las ecuaciones.
Recordatorio
La forma general de una ecuación de segundo nivel es:
ax^2 + bx + c = 0
a Distinto de 0
Por tranquilidad, resolveremos la ecuación de 3 maneras diversas según los valores de los coeficientes b y c.
Se llama discriminante, Δ a:
Δ= b^2 -4ac
El símbolo de Δ nos posibilita conocer el tipo de resoluciones de la ecuación en tres casos:
• Un primer caso es que Δ>0, hay 2 resoluciones reales diversas.
• En el caso de que Δ=0, hay 2 resoluciones reales equivalentes.
• Si Δ 0
El discriminante es positivo, de esta forma que la ecuación tiene 2 resoluciones reales diversas.
Problema 1
Determinar el tipo y número de resoluciones de la ecuación
X^2 + X +1 =0
Solución
Calculamos el discriminante
Δ= b^2 -4ac
Como los coeficientes son a=1a=1, b=1b=1 y c=1c=1, el discriminante es
Δ= b^2 -4ac
= 1^2 – 4*1*1 =
= 1 – 4 = -3
El discriminante es negativo, de esta forma que la ecuación no posee resoluciones reales (tiene 2 resoluciones complicadas distintas).
Problema 2
Determinar el tipo y número de resoluciones de la ecuación
X^2 – 4X + 4 =0
Solución
Calculamos el discriminante
Δ= b^2 -4ac
Como los coeficientes son a=1, b=−4 y c=4, el discriminante es
Δ= b^2 -4ac
= (-4)^2 – 4*1*4=
= 16 -16 = 0
El discriminante es negativo, de esta forma que la ecuación tiene 2 resoluciones reales equivalentes.
Problema 3
Resolver la ecuación de segundo nivel inconclusa
X^2+4X=0
Es una ecuación inconclusa. Factorizamos para calcular las resoluciones:
X^2+4X=0
X(X+4)=0
X=0, X=-4
La ecuación tiene 2 resoluciones reales diversas: 0 y −4.
Problema 4
Encontrar las raíces de la funcionalidad polinómica de segundo nivel
f(x) = X^2-18
Las raíces del polinomio f son los valores de x para los que f(x) es 0, o sea, son las resoluciones de la ecuación
X^2-18=0
La ecuación es inconclusa. La resolvemos:
X^2 – 18=0
X^2 = 18
X= +/- Raiz(18)