Las areas de figuras comprende la superficie o extensión dentro de una figura, lo cual se expresa en unidades de medida que denominamos superficiales.
Las principales areas de las figuras planas que existen son las siguientes:
- Area de un triángulo.
- Area de un cuadrado.
- Area de un rectángulo.
- Area de un rombo.
- Area del romboide.
- Area del trapecio.
A continuación se pueden ver cuatros ejercicios de areas de figuras planas:
Ejercicio 1 areas de figuras: Area de un rectángulo

Primeramente debemos tener el rectángulo expresado en metros, para lo cual transformamos 7 decímetros a metros sabiendo que un decímetro tiene una equivalencia de 0,1 de metros por lo que 7 decímetros = 0,7 metros.
Así mismo transformaremos 40 centímetros sabiendo que 100 centímetros tiene una equivalencia de 1 metro por lo que 40 centímetros = 0,4 metros.
Por lo tanto, los datos que tendremos para resolver el ejercicio son los siguientes:
Base= b= 7 dm = 0,7 m
Altura = h= 40 cm = 0,4 m
Considerando que la fórmula del rectángulo es:
Area = A= b*h
Area = A= b*h = (0,7m)(0,4m) = 0,28 m2
Por lo cual es área es de 0,28 metros cuadrados.
HAGA CLICK PARA VER EJERCICIOS DE SISTEMAS DE ECUACIONES
Ejercicio 2 areas de figuras: Area de un Cuadrado

Primeramente debemos tener el cuadrado expresado en metros, para lo cual transformamos 150 milímetros a metros sabiendo que 1000 milímetros tiene una equivalencia de 1 metro por lo que 150 milímetros = 0,15 metros.
Por lo tanto, los datos que tendremos para resolver el ejercicio son los siguientes:
Lado = L= 150 mm = 0,15 m
Considerando que la fórmula del área del cuadrado es:
Área = A = L2
Área = A = L2 = (0,15 m)2 = 0,0225 m2
Por lo cual es área es de 0,0225 metros cuadrados.
Ejercicio 3 areas de figuras: Area de un Triangulo

Primeramente debemos tener el triángulo expresado en decímetros, para lo cual transformamos 35 decametros a metros sabiendo que un decametro tiene una equivalencia de 10 de metros por lo que 35 decametros = 350 metros.
Así mismo transformaremos 2,5 hectómetros sabiendo que 100 metros tiene una equivalencia de 1 hectómetro por lo que 2,5 hectómetros = 250 metros.
Por lo tanto, los datos que tendremos para resolver el ejercicio son los siguientes:
Base= b= 350 metros
Altura = h= 250 metros
Considerando que la fórmula del triángulo es:
Area = A= (b*h)/2
Area = A = (b*h)/2 = (350 m)(250 m)/2 = 43750 m2
Por lo cual es área es de 43750 metros cuadrados.
Ejercicio 4 áreas de figuras: Área de un Trapecio
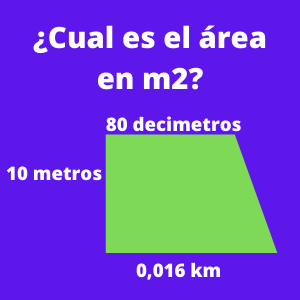
Primeramente debemos tener el trapecio expresado en metros, para lo cual transformamos 80 decímetros a metros sabiendo que un decímetro tiene una equivalencia de 0,1 de metros por lo que 80 decímetros = 8 metros.
Así mismo transformaremos 0,016 kilómetros sabiendo que 1000 metros tiene una equivalencia de 1 kilómetro por lo que 0,016 kilómetros = 16 metros.
Por lo tanto, los datos que tendremos para resolver el ejercicio son los siguientes:
Base Mayor = B= 0,016 Km = 16 m
Base Menor = b = 80 dm = 8 m
Altura = h = 10 m
Considerando que la fórmula del trapecio es:
Area = A= (B+b)*h/2
Area = A = (B+b)*h/2 = (16 m + 8 m)*(10 m)/2 = (24 m)(5 m) = 120 m2
Por lo cual es área es de 120 metros cuadrados.

