Cuando se habla de figuras geometricas nos estamos refiriendo a superficies planas delimitadas por líneas que pueden ser curvas o rectas. Una de las figuras geometricas más conocidas es el triangulo.
El triángulo se denomina así porque este tiene tres lados y este resulta de unir tres puntos y donde se pueden ver tres líneas en forma de recta. Donde se cruzan dos líneas se llaman vértices.
Uno de los triángulos más conocidos es el triangulo rectángulo; el cual esta compuesto por dos catetos y una hipotenusa. Los triángulos rectángulos se resuelven mediante el teorema de pitágoras que tienen la siguiente fórmula:
(Hipotenusa)^2 = (Cateto1)^2 + (Cateto2)^2
A continuación se pueden ver tres figuras geometricas para resolver:
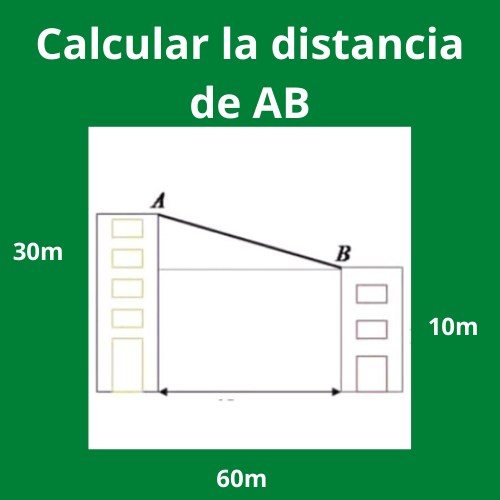
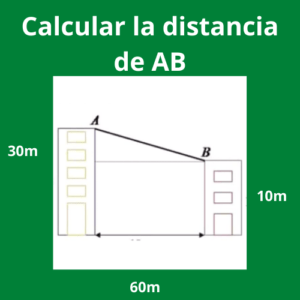
Ejercicio 1: Calcular la distancia de AB
Para calcular la distancia AB del triángulo, se necesita saber el valor del otro cateto y de la hipotenusa. Al ser un triángulo rectángulo se puede aplicar el teorema de Pitágoras.
Un cateto como se puede observar da 40 metros, el otro cateto es la diferencia de los dos edificios que se ven en la gráfica; es decir 25 metros – 15 metros = 10 metros.
El teorema de Pitágoras dice que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de sus catetos. Por tanto, en el siguiente triangulo tendremos:
(Hipotenusa)^2 = (Cateto1)^2 + (Cateto2)^2
(Hipotenusa)^2 = (40)^2 + (10)^2
(Hipotenusa)^2 = 1600 + 100
(Hipotenusa)^2 = 1700
Hipotenusa = Raíz(1700)
Por lo que la hipotenusa tendrá un valor de Hipotenusa = 41,23
HAGA CLICK PARA VER EJERCICIOS DE SISTEMAS DE ECUACIONES
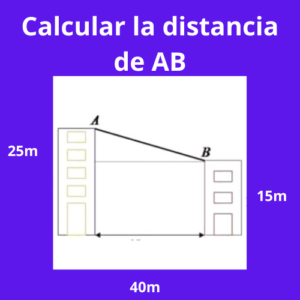
Ejercicio 2: Calcular la distancia de AB
Para calcular la distancia AB del triángulo, se necesita saber el valor del otro cateto y de la hipotenusa. Al ser un triángulo rectángulo se puede aplicar el teorema de Pitágoras.
Un cateto como se puede observar da 60 metros, el otro cateto es la diferencia de los dos edificios que se ven en la gráfica; es decir 30 metros – 10 metros = 20 metros.
El teorema de Pitágoras dice que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de sus catetos. Por tanto, en el siguiente triangulo tendremos:
(Hipotenusa)^2 = (Cateto1)^2 + (Cateto2)^2
(Hipotenusa)^2 = (60)^2 + (20)^2
(Hipotenusa)^2 = 3600 + 400
(Hipotenusa)^2 = 4000
Hipotenusa = Raíz(4000)
Por lo que la hipotenusa tendrá un valor de Hipotenusa = 63,24
HAGA CLICK PARA VER EJERCICIOS DE PROGRESIONES
Ejercicio 3: Calcular la distancia de AB
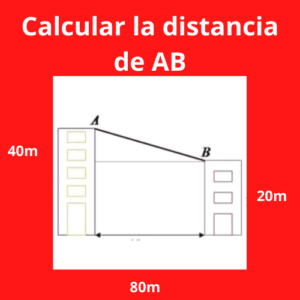
Para calcular la distancia AB del triángulo, se necesita saber el valor del otro cateto y de la hipotenusa. Al ser un triángulo rectángulo se puede aplicar el teorema de Pitágoras.
Un cateto como se puede observar da 80 metros, el otro cateto es la diferencia de los dos edificios que se ven en la gráfica; es decir 40 metros – 20 metros = 20 metros.
El teorema de Pitágoras dice que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de sus catetos. Por tanto, en el siguiente triangulo tendremos:
(Hipotenusa)^2 = (Cateto1)^2 + (Cateto2)^2
(Hipotenusa)^2 = (80)^2 + (20)^2
(Hipotenusa)^2 = 6400 + 400
(Hipotenusa)^2 = 6800
Hipotenusa = Raíz(6800)
Por lo que la hipotenusa tendrá un valor de Hipotenusa = 82,46