En el presente artículo resolveremos ejercicios de la ley Ley de cosenos. La ley de cosenos se aplica en dos casos. El primer caso es sabiendo 2 lados y el angulo entre ellos y el segundo caso es sabiendo los tres lados. Veamos a continuación algunos ejemplos con el segundo caso:
Para esto se utilizara la siguiente fórmula:
Cos A = a2 – b2 – c2/ – 2bc Cos A
Ejercicio 1: ejercicios de ley de cosenos: Calcular el valor de los angulos de un triangulo cuyos lados tienen las siguientes medidas a=12 m, b=25m, c=14m?
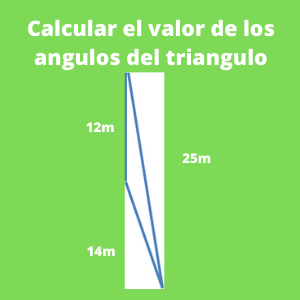
Inicialmente denominaremos el nombre de cada variable,llamandolas de la siguiente forma:
a= 12m
b= 25m
c= 14m
En base a la siguiente fórmula calcularemos el ángulo que intercepta a los lados de 25m y 14m.
Cos A = (a2 – b2 – c2)/-2bc
Reemplazando los valores tendremos:
Cos A = ((12m)2 – (25m)2 – (14m)2)/ – 2(25m)(14m)
Cos A = (144 – 625 – 196)/ – 700
Cos A = – 677/-700
Cos A = 0,9671
A = 14,73 grados
Ahora procederemos a calcular, el ángulo que intercepta a los lados de 12m y 14m, obeniendo lo siguiente:
Cos B = (b2 – a2 – c2)/-2ac
Reemplazando los valores tendremos:
Cos B = ((25m)2 – (12m)2 – (14m)2)/( – 2(12m)(14m)
Cos B = (625 – 144 – 196)/ – 336
Cos B = 285/-336
Cos B = -0,8482
B = 148,02 grados
Finalmente procederemos a calcular, el tercer ángulo interceptando a los lados de 12m y 25m, obeniendo lo siguiente:
Cos C = (c2 – a2 – b2)/-2ab
Reemplazando los valores tendremos:
Cos C = (14m)2 – (12m)2 – (25m)2/ – 2(12m)(25m)
Cos C = (196 -144 – 625)/ – 600
Cos C = – 573/-600
Cos C = 0,9555
C = 17,25 grados
Realizando la comprobación, podemos ver que la suma de los tres ángulos de un valor de 180 grados.
HAGA CLICK PARA VER EJERCICIOS DE PROGRESIONES
Ejercicio 2: ejercicios de ley de cosenos: Calcular el valor de los angulos de un triangulo cuyos lados tienen las siguientes medidas a=5 m, b=4m, c=7m?
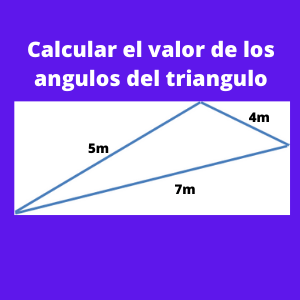
Inicialmente denominaremos el nombre de cada variable,llamandolas de la siguiente forma:
a= 5m
b= 4m
c= 7m
En base a la siguiente fórmula calcularemos el ángulo que intercepta a los lados de 4m y 7m.
Cos A = (a2 – b2 – c2)/-2bc
Reemplazando los valores tendremos:
Cos A = ((5m)2 – (4m)2 – (7m)2)/ – 2(4m)(7m)
Cos A = (25 – 16 – 49)/ – 56
Cos A = – 40/-56
Cos A = 0,7142
A = 44,42 grados
Ahora procederemos a calcular, el ángulo que intercepta a los lados de 5m y 7m, obeniendo lo siguiente:
Cos B = (b2 – a2 – c2)/-2ac
Reemplazando los valores tendremos:
Cos B = ((4m)2 – (5m)2 – (7m)2)/( – 2(5m)(7m)
Cos B = (16 – 25 – 49)/ – 70
Cos B = -58/-70
Cos B = 0,8285
B = 34,04 grados
Finalmente procederemos a calcular, el tercer ángulo interceptando a los lados de 5m y 4m, obeniendo lo siguiente:
Cos C = (c2 – a2 – b2)/-2ab
Reemplazando los valores tendremos:
Cos C = (7m)2 – (5m)2 – (4m)2/ – 2(5m)(4m)
Cos C = (49 -25 – 16)/ – 40
Cos C = 8/-40
Cos C = -0,2
C = 101,53 grados
Realizando la comprobación, podemos ver que la suma de los tres ángulos de un valor de 180 grados.
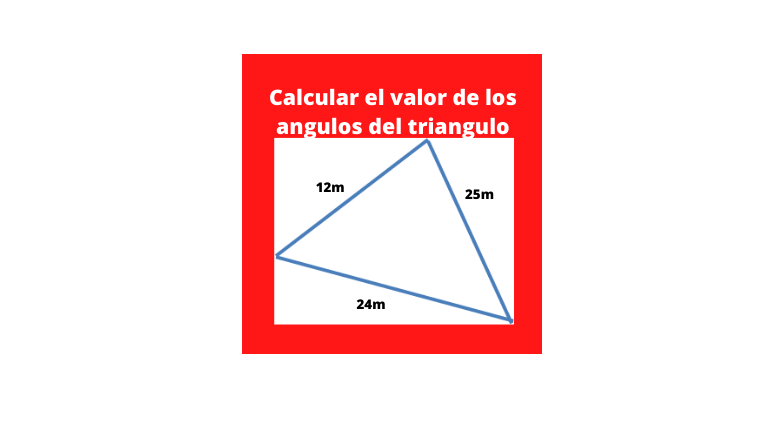
Ejercicio 3: ejercicios de ley de cosenos: Calcular el valor de los angulos de un triangulo cuyos lados tienen las siguientes medidas a=12 m, b=25m, c=24m?

Inicialmente denominaremos el nombre de cada variable,llamandolas de la siguiente forma:
a= 12m
b= 25m
c= 24m
En base a la siguiente fórmula calcularemos el ángulo que intercepta a los lados de 25m y 24m.
Cos A = (a2 – b2 – c2)/-2bc
Reemplazando los valores tendremos:
Cos A = ((12m)2 – (25m)2 – (24m)2)/ – 2(25m)(24m)
Cos A = (144 – 625 – 576)/ – 1200
Cos A = – 1057/-1200
Cos A = 0,8819
A = 28,19 grados
Ahora procederemos a calcular, el ángulo que intercepta a los lados de 12m y 24m, obeniendo lo siguiente:
Cos B = (b2 – a2 – c2)/-2ac
Reemplazando los valores tendremos:
Cos B = ((25m)2 – (12m)2 – (24m)2)/( – 2(12m)(24m)
Cos B = (625 – 144 – 576)/ – 576
Cos B = -95/-576
Cos B = 0,1649
B = 80,51 grados
Finalmente procederemos a calcular, el tercer ángulo interceptando a los lados de 12m y 25m, obeniendo lo siguiente:
Cos C = (c2 – a2 – b2)/-2ab
Reemplazando los valores tendremos:
Cos C = (24m)2 – (12m)2 – (25m)2/ – 2(12m)(25m)
Cos C = (576 -144 – 625)/ – 600
Cos C = -193/-600
Cos C = 0,3216
C = 71,24 grados
Realizando la comprobación, podemos ver que la suma de los tres ángulos de un valor de 180 grados.
HAGA CLICK PARA VER EJERCICIOS DE ACERTIJOS
Ejercicio 4: ejercicios de ley de cosenos: Calcular el valor de los angulos de un triangulo cuyos lados tienen las siguientes medidas a=11 m, b=9m, c=15m?
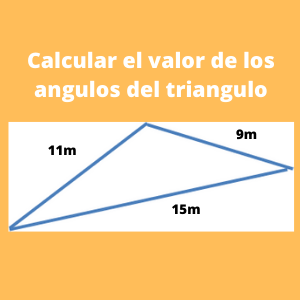
Inicialmente denominaremos el nombre de cada variable,llamandolas de la siguiente forma:
a= 11m
b= 9m
c= 15m
En base a la siguiente fórmula calcularemos el ángulo que intercepta a los lados de 9m y 15m.
Cos A = (a2 – b2 – c2)/-2bc
Reemplazando los valores tendremos:
Cos A = ((11m)2 – (9m)2 – (15m)2)/ – 2(9m)(15m)
Cos A = (121 – 81 – 225)/ – 270
Cos A = – 185/-270
Cos A = 0,6851
A = 46,75 grados
Ahora procederemos a calcular, el ángulo que intercepta a los lados de 11m y 15m, obeniendo lo siguiente:
Cos B = (b2 – a2 – c2)/-2ac
Reemplazando los valores tendremos:
Cos B = ((9m)2 – (11m)2 – (15m)2)/( – 2(11m)(15m)
Cos B = (81 – 121 – 225)/ – 310
Cos B = -265/-310
Cos B = 0,8548
B = 31,25 grados
Finalmente procederemos a calcular, el tercer ángulo interceptando a los lados de 11m y 9m, obeniendo lo siguiente:
Cos C = (c2 – a2 – b2)/-2ab
Reemplazando los valores tendremos:
Cos C = (15m)2 – (11m)2 – (9m)2/ – 2(11m)(9m)
Cos C = (225 -121 – 81)/ – 198
Cos C = 23/-198
Cos C = -0,1161
C = 96,67 grados
Realizando la comprobación, podemos ver que la suma de los tres ángulos de un valor de 180 grados.