En el presente artículo resolveremos ejercicios de trigonometria basica aplicando la ley Ley de cosenos. La ley de cosenos se aplica en dos casos. El primer caso es sabiendo 2 lados y un angulo de un triangulo entre ellos y el segundo caso es sabiendo los tres lados. Veamos a continuación algunos cursos de matematicas con el primer caso:
Para esto se utilizara la siguiente fórmula:
Cos A = a2 – b2 – c2/ – 2bc
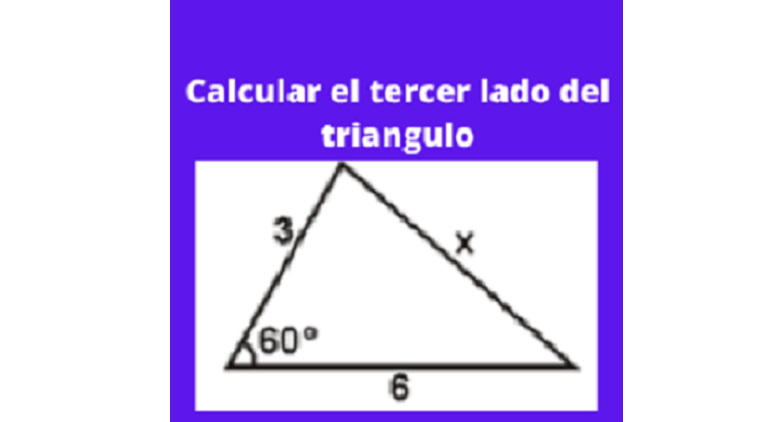
Ejercicio 1 trigonometria basica: ejercicios de ley de cosenos: Calcular el valor de X (tercer lado del triángulo), si los otros lados tienen las siguientes medidas b=3 m, c= 6 m y el ángulo Angulo A= 60?

Inicialmente denominaremos el nombre de cada variable,llamandolas de la siguiente forma:
b= 3m
c= 6m
Angulo A = A = 60
En base a la siguiente fórmula calcularemos el tercer lado del triangulo.
Cos A = (a2 – b2 – c2)/-2bc
Reemplazando los valores tendremos:
Cos 60 = ((a)2 – (3)2 – (6)2)/ – 2(3)(6)
Cos 60 = ((a)2 – 9 – 36)/ – 2(3)(6)
Cos 60 = (a2 – 45)/ – 36
-36*Cos 60 = a2 – 45
a2 = 45 -36*Cos 60
a2 = 45 -36*0,5
a2 = 45 -18
a2 = 27
a = 3RAIZ(3)
Por lo que el tercer lado medira 3RAIZ(3) metros
HAGA CLICK PARA VER EJERCICIOS DE ACERTIJOS
Ejercicio 2 trigonometria basica: ejercicios de ley de cosenos: Calcular el valor de X (tercer lado del triángulo), si los otros lados tienen las siguientes medidas b=4 m, c= 7 m y el ángulo Angulo A= 112?
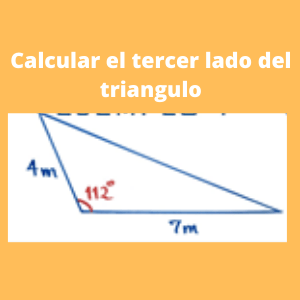
Cursos de matematicas. Inicialmente denominaremos el nombre de cada variable,llamandolas de la siguiente forma:
b= 4m
c= 7m
Angulo A = A = 112
En base a la siguiente fórmula calcularemos el tercer lado del triangulo.
Cos A = (a2 – b2 – c2)/-2bc
Reemplazando los valores tendremos:
Cos 112 = ((a)2 – (4)2 – (7)2)/ – 2(4)(7)
Cos 112 = ((a)2 – 16 – 49)/ – 2(4)(7)
Cos 112 = (a2 – 65)/ – 56
-56*Cos 112 = a2 – 65
a2 = 65 -56*Cos 112
a2 = 65 -56*-0,3746
a2 = 65 +20,98
a2 = 85,98
a = 9,27m
Por lo que el tercer lado medira a= 9,27 metros
Ejercicio 3: ejercicios de ley de cosenos: Calcular el valor de X (tercer lado del triángulo), si los otros lados tienen las siguientes medidas b=7 m, c= 12 m y el ángulo Angulo A= 40?
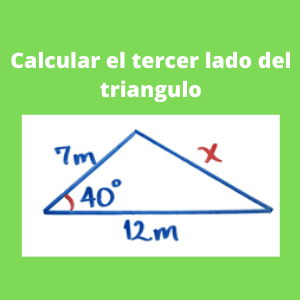
Inicialmente denominaremos el nombre de cada variable,llamandolas de la siguiente forma:
b= 7m
c= 12m
Angulo A = A = 40
En base a la siguiente fórmula calcularemos el tercer lado del triangulo.
Cos A = (a2 – b2 – c2)/-2bc
Reemplazando los valores tendremos:
Cos 40 = ((a)2 – (7)2 – (12)2)/ – 2(7)(12)
Cos 40 = ((a)2 – 49 – 144)/ – 2(7)(12)
Cos 40 = (a2 – 193)/ – 168
-168*Cos 40 = a2 – 193
a2 = 193 -168*Cos 40
a2 = 193 -168*0,766
a2 = 193 -128,7
a2 = 64,3
a = 8,01 m
Por lo que el tercer lado medira 8,01 metros
HAGA CLICK PARA VER EJERCICIOS DE PERMUTACION
Ejercicio 4: ejercicios de ley de cosenos: Calcular el valor de X (tercer lado del triángulo), si los otros lados tienen las siguientes medidas a=13 cm, c= 19 cm y el ángulo Angulo A= 55?
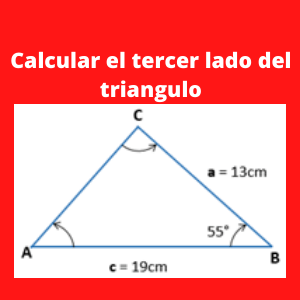
Inicialmente denominaremos el nombre de cada variable,llamandolas de la siguiente forma:
a= 13cm
c= 19cm
Angulo B = B = 55
En base a la siguiente fórmula calcularemos el tercer lado del triangulo.
Cos B = (b2 – a2 – c2)/-2ac
Reemplazando los valores tendremos:
Cos 55 = ((b)2 – (13)2 – (19)2)/ – 2(13)(19)
Cos 55 = ((b)2 – 169 – 361)/ – 2(13)(19)
Cos 55 = (b2 – 530)/ – 494
-494*Cos 55 = b2 – 530
b2 = 530 -494*Cos 55
b2 = 530 -494*0,5736
b2 = 530 -283,35
b2 = 246,65
b = 15,7
Por lo que el tercer lado medira 15,7 cm