La geometria analítica esta dedicada a estudiar las figuras, sus distancias, sus áreas, ángulos de inclinación, etc. Es un análisis más detallado que el de la trigonometría o solo el de la geometría.
La Geometría es la parte de las Matemáticas que estudia las idealizaciones del espacio en términos de las propiedades y medidas de las figuras geométricas. La geometria analítica es utilizada en el campo de la matemática e ingeniería, para aplicaciones en planeación, estructura, sanitario y eléctrico, pero también en la administración y economía.
A continuación se puede apreciar 3 dificiles ejercicios de geometria analítica:
Ejercicio 1 geometria analítica: Determinar el ángulo solicitado
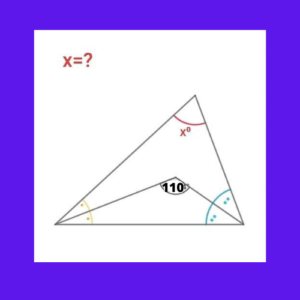
Inicialmente se determinaran las variables del ejercicio, las cuales son:
A= ángulo de color naranja
B= ángulo de color celeste
A partir de las mencionadas variables, establecemos un sistema de dos ecuaciones (conociendo que la suma de ángulos de un triángulo es de 18 grados):
X+2A+2B=180
110+A+B=180
Despejamos A+B en la segunda ecuación obteniendo:
A+B=70
Reemplazamos el valor de A+B en la primera ecuación obteniendo lo siguiente:
X+2(A+B)=180
X+2(70)=180
X+140=180
Por lo tanto el valor de X es X=40 grados
HACE CLICK PARA VER 200 EJERCICIOS DE ALGEBRA
Ejercicio 2 geometria analítica: Determinar el ángulo solicitado

Inicialmente se determinaran las variables del ejercicio, las cuales son:
A= ángulo de color naranja
B= ángulo de color celeste
A partir de las mencionadas variables, establecemos un sistema de dos ecuaciones (conociendo que la suma de ángulos de un triángulo es de 18 grados):
X+2A+2B=180
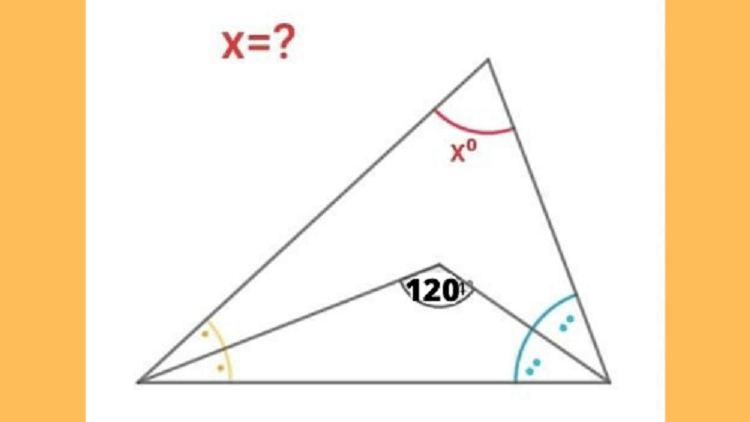
120+A+B=180
Despejamos A+B en la segunda ecuación obteniendo:
A+B=60
Reemplazamos el valor de A+B en la primera ecuación obteniendo lo siguiente:
X+2(A+B)=180
X+2(60)=180
X+120=180
Por lo tanto el valor de X es X=60 grados
HACE CLICK PARA VER EJERCICIOS DE SISTEMAS DE ECUACIONES
Ejercicio 3: Determinar el ángulo solicitado
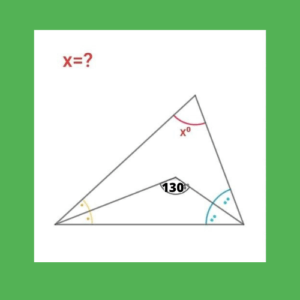
Inicialmente se determinaran las variables del ejercicio, las cuales son:
A= ángulo de color naranja
B= ángulo de color celeste
A partir de las mencionadas variables, establecemos un sistema de dos ecuaciones (conociendo que la suma de ángulos de un triángulo es de 18 grados):
X+2A+2B=180
130+A+B=180
Despejamos A+B en la segunda ecuación obteniendo:
A+B=50
Reemplazamos el valor de A+B en la primera ecuación obteniendo lo siguiente:
X+2(A+B)=180
X+2(50)=180
X+100=180
Por lo tanto el valor de X es X=80 grados