Un triangulo es el polígono que resulta de unir 3 puntos con líneas rectas. Todo triángulo tiene 3 lados, 3 vértices (es el punto común entre dos lados) y 3 ángulos.
Los tipos de triángulos que existen son: el triángulo rectángulo, Triángulo equilátero, Triángulo isósceles y Triángulo escaleno siendo el más importante y conocido el triangulo rectángulo.
Los principales elementos que existen cuando se habla de un triángulo rectángulo, que es el triángulo más conocido y utilizado son:
- Catetos: lados del triángulo que forman el ángulo recto.
- Hipotenusa: lado mayor del triángulo opuesto al ángulo recto.
- Ángulo recto: ángulo de 90º.
- Ángulos agudos: Ángulos del triángulo menores de 90º.
A continuación se pueden apreciar 3 desafiantes ejercicios para calcular la altura del triangulo:
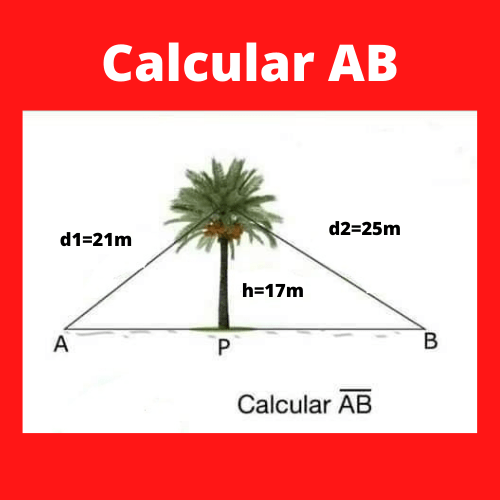
Ejercicio 1 triangulo: Determinar el valor de la longitud AB
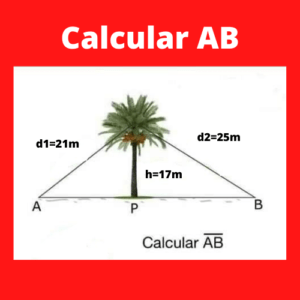
Para calcular el valor de AB que forma parte de un triángulo, esta se dividirá en dos triángulos.
Triangulo A
Es un triángulo rectángulo, este se resuelve mediante la siguiente fórmula:
Hipotenusa^2= (Cateto Opuesto)^2+(Cateto Adyacente)^2
Despejando el cateto adyacente tenemos:
(Cateto Adyacente)^2= Hipotenusa^2 – (Cateto Opuesto)^2
Por lo que tenemos:
(Cateto Adyacente)^2= 21^2-17^2
=441-289=152
=12,32883
Triangulo B
Es un triángulo rectángulo, este se resuelve mediante la siguiente fórmula:
Hipotenusa^2= (Cateto Opuesto)^2+(Cateto Adyacente)^2
Despejando el cateto adyacente tenemos:
(Cateto Adyacente)^2= Hipotenusa^2 – (Cateto Opuesto)^2
Por lo que tenemos:
(Cateto Adyacente)^2= 25^2-17^2
=625-289=336
=18,3303
Por lo que finalmente podemos obtener el valor AB que es de AB=30,65913
VER EJERCICIOS DE TRIGONOMETRIA
Ejercicio 2 triangulo: Determinar el valor de la longitud AB
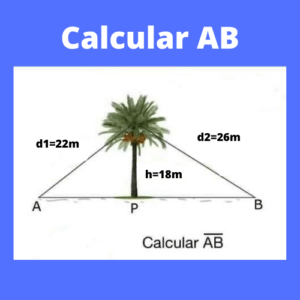
Para calcular el valor de AB que forma parte de un triángulo, esta se dividirá en dos triángulos.
Triangulo A
Es un triángulo rectángulo, este se resuelve mediante la siguiente fórmula:
Hipotenusa^2= (Cateto Opuesto)^2+(Cateto Adyacente)^2
Despejando el cateto adyacente tenemos:
(Cateto Adyacente)^2= Hipotenusa^2 – (Cateto Opuesto)^2
Por lo que tenemos:
(Cateto Adyacente)^2= 22^2-18^2
=484-324=160
=12,64911
Triangulo B
Es un triángulo rectángulo, este se resuelve mediante la siguiente fórmula:
Hipotenusa^2= (Cateto Opuesto)^2+(Cateto Adyacente)^2
Despejando el cateto adyacente tenemos:
(Cateto Adyacente)^2= Hipotenusa^2 – (Cateto Opuesto)^2
Por lo que tenemos:
(Cateto Adyacente)^2= 26^2-18^2
=676-324=352
=18,7616
Por lo que finalmente podemos obtener el valor AB que es de AB=31,4
VER LIBROS DE ALGEBRA DE BALDOR
Ejercicio 3: Determinar el valor de la longitud AB
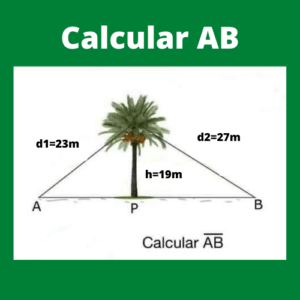
Para calcular el valor de AB que forma parte de un triángulo, esta se dividirá en dos triángulos.
Triangulo A
Es un triángulo rectángulo, este se resuelve mediante la siguiente fórmula:
Hipotenusa^2= (Cateto Opuesto)^2+(Cateto Adyacente)^2
Despejando el cateto adyacente tenemos:
(Cateto Adyacente)^2= Hipotenusa^2 – (Cateto Opuesto)^2
Por lo que tenemos:
(Cateto Adyacente)^2= 23^2-19^2
=529-361=168
=12,96148
Triangulo B
Es un triángulo rectángulo, este se resuelve mediante la siguiente fórmula:
Hipotenusa^2= (Cateto Opuesto)^2+(Cateto Adyacente)^2
Despejando el cateto adyacente tenemos:
(Cateto Adyacente)^2= Hipotenusa^2 – (Cateto Opuesto)^2
Por lo que tenemos:
(Cateto Adyacente)^2= 27^2-19^2
=729-361=368
=19,1833
Por lo que finalmente podemos obtener el valor AB que es de AB=32,14481