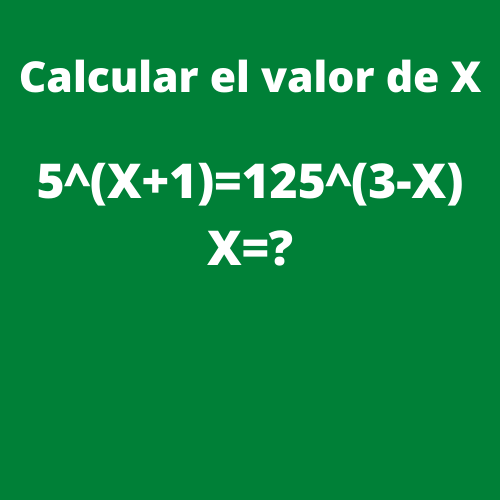A continuación se pueden apreciar 3 interesantes ejercicios de álgebra para resolver:
Ejercicio 1: Sí 2^(X+1)=8^(3-X), X=?
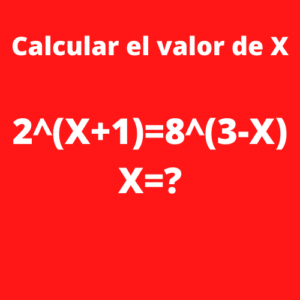
Para poder calcular el valor de X de la siguiente ecuación 2^(X+1)=8^(3-X), primero se buscara que las bases de las mismas sean iguales por lo que tendremos 2^(X+1)= 2^ [3(3-X)]. Como las bases son iguales los exponentes también serán igual resumiendo la expresión a (X+1)= 3(3-X). Se realizarán las siguientes operaciones para despejar X:
X+1= 9-3X
4X=8
Por lo que el valor de X es de X=2
VER LIBROS DE ALGEBRA DE BALDOR
Ejercicio 2: Si 3^(X+5)=27^(7-X), X=?

Para poder calcular el valor de X de la siguiente ecuación 3^(X+5)=27^(7-X), primero se buscara que las bases de las mismas sean iguales por lo que tendremos 3^(X+5)= 3^ [3(7-X)]. Como las bases son iguales los exponentes también serán igual resumiendo la expresión a (X+5)= 3(7-X). Se realizarán las siguientes operaciones para despejar X:
X+5= 21-3X
4X=16
Por lo que el valor de X es de X=4
VER EJERCICIOS DE PROGRESIONES
Ejercicio 3: Si 5^(X+1)=125^(3-X), X=?

Para poder calcular el valor de X de la siguiente ecuación 5^(X+1)=125^(3-X), primero se buscara que las bases de las mismas sean iguales por lo que tendremos 5^(X+1)= 5^ [3(3-X)]. Como las bases son iguales los exponentes también serán igual resumiendo la expresión a (X+1)= 3(3-X). Se realizarán las siguientes operaciones para despejar X:
X+1= 9-3X
4X=8
Por lo que el valor de X es de X=2