Para poder calcular determinante de una matriz, necesitamos que su dimensión tenga el mismo número de filas (m) y columnas (n) lo que es conocida con el nombre de matriz cuadrada, caso contrario no existirá una respuesta.
En el presente artículo veremos cómo calcular determinante de orden 3 por la regla de Sarrus, la cual es una matriz de dimensión 3×3. La regla de Sarrus establece que para calcular determinante de orden 3 tenemos que sumar el producto de los elementos de la diagonal y de sus diagonales paralelas tal como se puede ver en la siguiente gráfica:
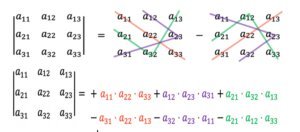
A continuación podemos apreciar tres ejercicios resueltos de determinantes de tamaño 3×3 por la Regla de Sarrus:
Ejercicio 1 Calcular determinante:

Para poder calcular determinante de la matriz por la Regla de Sarrus, se necesita inicialmente colocar las dos primeras columnas en el lado derecho de la matriz y sumar el producto de los elementos de la diagonal y de sus diagonales paralelas obteniendo de esta manera la siguiente ecuación:
(11*X*3 + 2*3*3 + 5*4*9) – (9*X*3 + 4*3*11 + 5*2*3) = 67
Para conocer a detalle las multiplicaciones a realizar ver la gráfica inicial del presente artículo. Ahora realizaremos operaciones, buscando despejar X obteniendo:
(33X + 18 + 180) – (27X + 132 + 30) = 67
33X + 18 + 180 – 27X – 132 – 30 = 67
33X + 198 – 27X – 162 = 67
6X + 36 = 67
6X = 31
Por lo que el valor de X será de:
X = 31/6
HACE CLICK PARA VER 100 EJERCICIOS DE ALGEBRA
Ejercicio 2 Calcular determinante:

Para poder calcular determinante de la matriz por la Regla de Sarrus, se necesita inicialmente colocar las dos primeras columnas en el lado derecho de la matriz y sumar el producto de los elementos de la diagonal y de sus diagonales paralelas obteniendo de esta manera la siguiente ecuación:
(2*X*6 + 4*4*15 + 12*4*7) – (7*X*15 + 4*4*2 + 12*4*6) = 54
Para conocer a detalle las multiplicaciones a realizar ver la gráfica inicial del presente artículo. Ahora realizaremos operaciones, buscando despejar X obteniendo:
(12X + 240 + 336) – (105X + 32 + 288) = 54
12X + 240 + 336 –105X – 32 – 288 = 54
12X + 576 –105X – 320 = 54
-93X + 256 = 54
93X = 202
Por lo que el valor de X será de:
X = 202/93
HACE CLICK PARA VER EJERCICIOS DE FRACCIONES
Ejercicio 3 Resolver la siguiente determinante:

Para poder calcular determinante de la matriz por la Regla de Sarrus, se necesita inicialmente colocar las dos primeras columnas en el lado derecho de la matriz y sumar el producto de los elementos de la diagonal y de sus diagonales paralelas obteniendo de esta manera la siguiente ecuación:
(7*1*X + 3*0*3 + 5*4*4) – (4*1*3 + 4*0*7 + 5*3*X) = 30
Para conocer a detalle las multiplicaciones a realizar ver la gráfica inicial del presente artículo. Ahora realizaremos operaciones, buscando despejar X obteniendo:
(7X + 0 + 80) – (12 + 0 + 15X) = 30
7X + 0 + 80 – 12 – 0 – 15X = 30
7X + 80 – 12 – 15X = 30
-8X + 68 = 30
8X = 38
Por lo que el valor de X será de:
X = 38/8

