En matemáticas, las funciones de la trigonometría generalmente incluyen términos que describen la medición de ángulos y triángulos, tal como seno, coseno, tangente, cotangente, secante y cosecante. En el siguiente artículo se verá ejercicios de funciones de la trigonometría.
En la trigonometría existen relaciones reciprocas y relaciones pitagóricas son las siguientes:
RELACIONES RECIPROCAS
1 senΘ = 1/cosecΘ
2 cosΘ = 1/secΘ
3 tgΘ = 1/ctgΘ
4 tgΘ = 1/ctgΘ
5 ctgΘ = cosΘ/senΘ
RELACIONES PITAGORICAS
6 sen2Θ + cos2Θ = 1
7 tg2Θ + 1= sec2Θ
8 1 + ctg2Θ= cosec2Θ
Las razones trigonométricas, con las cuales trabajaremos en los próximos tres ejercicios son las siguiente:
Nombre Abreviatura
SENO sen
COSENO cos
TANGENTE tg
COTANGENTE ctg
SECANTE sec
COSECANTE cosec
senΘ = cateto opuesto / hipotenusa
cosΘ =cateto adyacente / hipotenusa
tgΘ = cateto opuesto / cateto adyacente
ctgΘ = cateto adyacente / cateto opuesto
secΘ = cateto adyacente / hipotenusa
cosecΘ = hipotenusa / cateto opuesto
Según estas definiciones, se tiene:
1 Las razones seno y coseno de un ángulo no pueden ser mayores que 1
2 Las razones secante y cosecante de un ángulo no pueden ser menores que uno
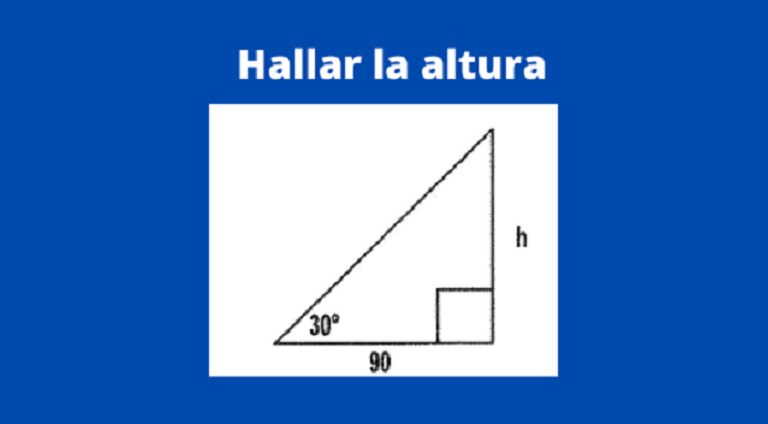
Ejercicio 1 funciones de la trigonometría: El ángulo de elevación del remate de una chimenea, a una distancia de 90 metros es de 30°. Hallar la altura.
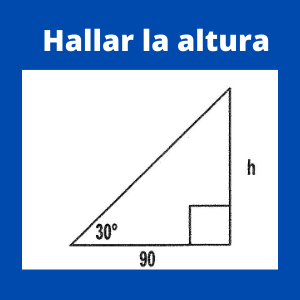
Para empezar se va a elaborar una primera ecuación a partir de la siguiente fórmula:
tgΘ = cateto opuesto / cateto adyacente
Logrando encontrar la siguiente formula:
tg30° = h/90
A partir de ahí, despejamos la altura, obteniendo el siguiente resultado:
h= 90*tg30°
h= 90*Raiz(3)/3
h= 30*Raiz(3) metros
Ejercicio 2 funciones de la trigonometría: Desde el puesto de vigía de un barco que tiene 48 m de altura se observa que el ángulo de depresión de un bote es de 30. Hallar la distancia del bote al barco.
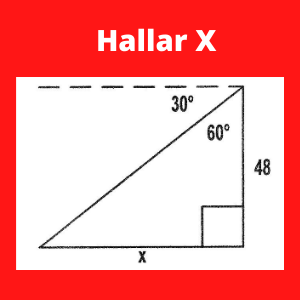
Para empezar se va a elaborar una primera ecuación a partir de la siguiente fórmula:
tgΘ = cateto opuesto / cateto adyacente
Logrando encontrar la siguiente formula:
Tg60° = x/48
A partir de ahí, despejamos la altura, obteniendo el siguiente resultado:
x= 48*tg60°
x= 48*Raiz(3) metros
Ejercicio 3: El ángulo de elevación de la parte superior de una torre es de 30 acercándose 100m se encuentra que el ángulo de elevación es de 60. Hallar la altura de la torre.
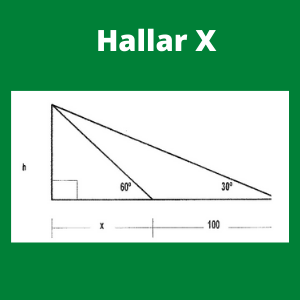
Para empezar se va a elaborar una primera ecuación a partir de la siguiente fórmula:
tgΘ = cateto opuesto / cateto adyacente
Logrando encontrar la siguiente formula:
Tg30° = h/(x+100)
A partir de ahí, despejamos la altura, obteniendo el siguiente resultado:
h= (x+100)/Raiz(3)
Así mismo, utilizamos una segunda ecuación utilizando el triángulo más pequeño, obteniendo lo siguiente:
Tg60° = h/x
h= x*Raiz(3)
Igualamos las dos ecuaciones, obteniendo lo siguiente:
(x+100)/Raiz(3) = x*Raiz(3)
Finalmente despejamos y calculamos x y h.
x+100 = 3x
100 = 2x
50 = x
h= 50*Raiz(3)
VER DIFERENTES EJERCICIOS DE MATEMATICAS
Ejercicio 4.- De un triángulo rectángulo ABC, se conocen a = 5 m y B = 41.7°. Resolver el triángulo
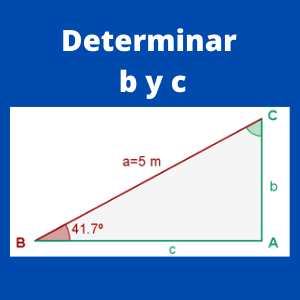
Primero se procederá a calcular b. Sabemos que:
senΘ = cateto opuesto / hipotenusa
Por lo que:
sen41,7*5= cateto opuesto = b
b= 3,325
Después se procederá a calcular c. Sabemos que:
cosΘ =cateto adyacente / hipotenusa
Por lo que:
cos41,7*5=cateto adyacente = c
c= 3,7331
VER DIFERENTES EJERCICIOS DE MATEMATICAS
Ejercicio 5.- De un triángulo rectángulo ABC, se conocen b = 3 m y B = 54.6°. Resolver el triángulo.
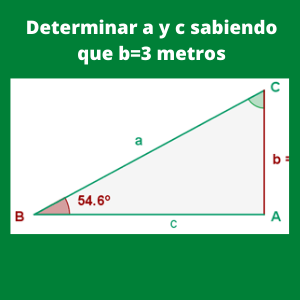
Primero se procederá a calcular a, que es la hipotenusa a partir del cateto opuesto que vale 3. Sabemos que:
senΘ = cateto opuesto / hipotenusa
Por lo que:
hipotenusa = senΘ / cateto opuesto
hipotenusa = 3/sen54,6
hipotenusa = 3,68
Después se procederá a calcular c. Sabemos que:
tgΘ =cateto opuesto / cateto adyacente
c viene a ser el cateto adyacente
Por lo que:
Tg54,6=cateto opuesto / cateto adyacente
Cateto adyacente = cateto opuesto / Tg54,6
Cateto adyacente = 3/Tg54,6
c= 2,14