La geometria es una parte de las matematicas que estudia los triangulos. Un triángulo es el polígono que resulta de unir 3 puntos con líneas rectas. Todo triángulo tiene 3 lados, 3 vértices (es el punto común entre dos lados) y 3 ángulos.
Los tipos de triángulos que existen son:
- Triángulo equilátero. Tiene todos los lados iguales (los ángulos internos miden 60 grados).
- Triángulo isósceles. Tiene dos lados iguales y uno diferente.
- Triángulo escaleno. Tiene todos los lados y ángulos distintos.
Los principales elementos que existen cuando se habla de un triángulo rectángulo, que es el triángulo más conocido y utilizado son:
- Catetos: lados del triángulo que forman el ángulo recto.
- Hipotenusa: lado mayor del triángulo opuesto al ángulo recto.
- Ángulo recto: ángulo de 90º.
- Ángulos agudos: Ángulos del triángulo menores de 90º.
A continuación se pueden observar 3 interesantes ejercicios de geometría resueltos:
Ejercicio 1 geometria: De la figura calcular X
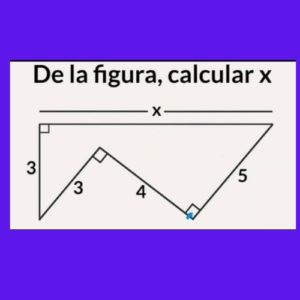
El valor de X lo obtendremos en base a la suma de dos distancias.
Primera Distancia
Para calcular el valor de X lo primero calculamos el valor de la parte inferior del triángulo que no tiene línea. Esta pertenece a un triángulo rectángulo, que se resuelve mediante la siguiente fórmula:
Hipotenusa^2= (Cateto Opuesto)^2+(Cateto Adyacente)^2
Remplazando los valores tenemos:
Hipotenusa^2= 4^2+3^2= 16+9 = 25
Hipotenusa= 5
Segunda Distancia
Sin embargo existe una distancia faltante, nuevamente utilizaremos el teorema de Pitágoras teniendo:
Hipotenusa^2= (Cateto Opuesto)^2+(Cateto Adyacente)^2
5^2= 3^2+(Cateto Adyacente)^2
25= 9+(Cateto Adyacente)^2
16= (Cateto Adyacente)^2
Cateto Adyacente=4
Por lo tanto, X valdra X=9 que es la suma de la primera y segunda distancia.
Ejercicio 2 geometria: De la figura calcular X
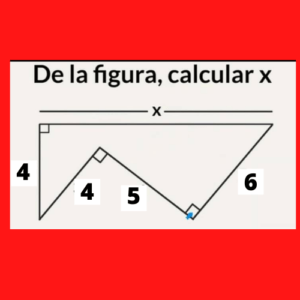
El valor de X lo obtendremos en base a la suma de dos distancias.
Primera Distancia
Para calcular el valor de X lo primero calculamos el valor de la parte inferior del triángulo que no tiene línea. Esta pertenece a un triángulo rectángulo, que se resuelve mediante la siguiente fórmula:
Hipotenusa^2= (Cateto Opuesto)^2+(Cateto Adyacente)^2
Remplazando los valores tenemos:
Hipotenusa^2= 4^2+5^2= 16+25= 41
Hipotenusa= Raiz(41)
Segunda Distancia
Sin embargo existe una distancia faltante, nuevamente utilizaremos el teorema de Pitágoras teniendo:
Hipotenusa^2= (Cateto Opuesto)^2+(Cateto Adyacente)^2
6^2= 4^2+(Cateto Adyacente)^2
36= 16+(Cateto Adyacente)^2
20= (Cateto Adyacente)^2
Cateto Adyacente=Raiz(20)
Por lo tanto, X valdra X=Raiz(41)+Raiz(20)= 10,87 que es la suma de la primera y segunda distancia.
VER TODO TIPO DE EJERCICIOS DE MATEMATICAS
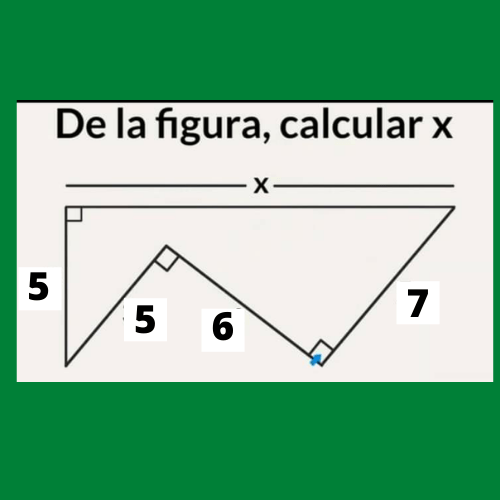
Ejercicio 3: De la figura calcular X
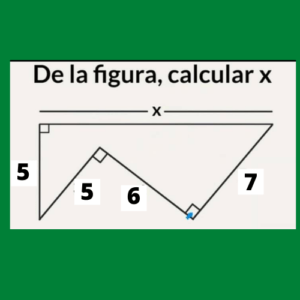
El valor de X lo obtendremos en base a la suma de dos distancias.
Primera Distancia
Para calcular el valor de X lo primero calculamos el valor de la parte inferior del triángulo que no tiene línea. Esta pertenece a un triángulo rectángulo, que se resuelve mediante la siguiente fórmula:
Hipotenusa^2= (Cateto Opuesto)^2+(Cateto Adyacente)^2
Remplazando los valores tenemos:
Hipotenusa^2= 5^2+6^2= 25+36= 71
Hipotenusa= Raiz(71)
Segunda Distancia
Sin embargo existe una distancia faltante, nuevamente utilizaremos el teorema de Pitágoras teniendo:
Hipotenusa^2= (Cateto Opuesto)^2+(Cateto Adyacente)^2
7^2= 5^2+(Cateto Adyacente)^2
49= 25+(Cateto Adyacente)^2
24= (Cateto Adyacente)^2
Cateto Adyacente=Raiz(24)
Por lo tanto, X valdra X=Raiz(71)+Raiz(24)= 13,33 que es la suma de la primera y segunda distancia.