Las formulas trigonometria más utilizadas son el área y el perímetro para diferentes figuras como son el cuadrado, rectángulo y triangulo.
Las funciones y=sinx, y=cosx, y=tg x. El seno (sen) es el cociente entre el cateto opuesto al ángulo y la hipotenusa. El coseno (cos) es el cociente entre el cateto adjunto al ángulo y la hipotenusa.
Las identidades trigonométricas nos permiten plantear una misma expresión de diferentes formas. Para simplificar expresiones algebraicas, usamos la factorización, denominadores comunes, etc. Pero para simplificar expresiones trigonométricas utilizaremos estas técnicas en conjunto con las identidades trigonométricas.
El seno de un ángulo α se define como la razón entre el cateto opuesto (a) y la hipotenusa (c). El coseno se define como la razón entre el cateto contiguo o cateto adyacente (b) y la hipotenusa (c). La tangente es la razón entre el cateto opuesto (a) y el cateto contiguo o cateto adyacente (b).
Las identidades trigonométricas fundamentales son las siguientes:
- Seno – coseno. cos² α + sen² α = 1.
- Secante – tangente. sec² α = 1 + tg² α
- Cosecante – cotangente. csc² α = 1 + ctg² α
- csc α = 1 / sen α
- sec α = 1 / cos α
- ctg α = 1 / tg α
A continuación se puede apreciar 3 ejercicios con las formulas trigonometria más utilizadas:
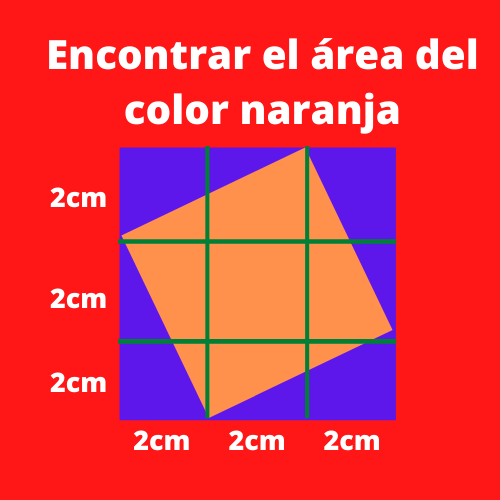
Ejercicio 1 formulas trigonometria: Encontrar el área del color naranja
Primero estableceremos variables para determinar uno de los lados del cuadrado de color naranja, las cuales serán las siguientes:
Hipotenusa= ?
Cateto Opuesto= 2 cm
Cateto Adyacente= 1 cm
Determinaremos la hipotenusa utilizando la siguiente fórmula:
Hipotenusa^2= Cateto Opuesto^2 + Cateto Adyacente^2
Reemplazamos los valores tendremos:
Hipotenusa^2= 2^2 + 1^2
Hipotenusa^2= 4 + 1
Hip^2= 5
Hipotenusa= Raiz(5)
El valor de la hipotenusa es el valor de uno de los lados del cuadrado. Para calcular el área del cuadrado utilizaremos la siguiente fórmula:
Area del cuadrado= Lado*Lado
Area del cuadrado= Raiz(5)* Raiz(5)=5
Por lo que el área del cuadrado es de 5 cm^2
HACE CLICK DESCARGA EL LIBRO ALGEBRA DE BALDOR
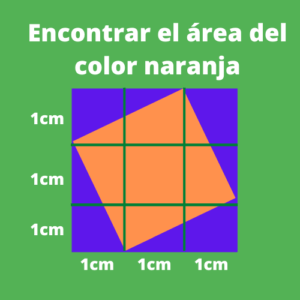
Ejercicio 2 formulas trigonometria: Encontrar el área del color naranja
Primero estableceremos variables para determinar uno de los lados del cuadrado de color naranja, las cuales serán las siguientes:
Hipotenusa= ?
Cateto Opuesto= 4 cm
Cateto Adyacente= 2 cm
Determinaremos la hipotenusa utilizando la siguiente fórmula:
Hipotenusa^2= Cateto Opuesto^2 + Cateto Adyacente^2
Reemplazamos los valores tendremos:
Hipotenusa^2= 4^2 + 2^2
Hipotenusa^2= 16 + 4
Hip^2= 20
Hipotenusa= Raiz(20)
El valor de la hipotenusa es el valor de uno de los lados del cuadrado. Para calcular el área del cuadrado utilizaremos la siguiente fórmula:
Area del cuadrado= Lado*Lado
Area del cuadrado= Raiz(20)* Raiz(20)=20
Por lo que el área del cuadrado es de 20 cm^2
HACE CLICK PARA DESCARGAR LIBROS DE CALCULO
Ejercicio 3: Encontrar el área del color naranja
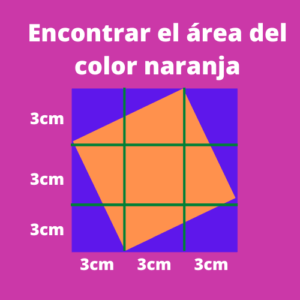
Primero estableceremos variables para determinar uno de los lados del cuadrado de color naranja, las cuales serán las siguientes:
Hipotenusa= ?
Cateto Opuesto= 6 cm
Cateto Adyacente= 3 cm
Determinaremos la hipotenusa utilizando la siguiente fórmula:
Hipotenusa^2= Cateto Opuesto^2 + Cateto Adyacente^2
Reemplazamos los valores tendremos:
Hipotenusa^2= 6^2 + 3^2
Hip^2= 36 + 9
Hipotenusa^2= 45
Hipotenusa= Raiz(45)
El valor de la hipotenusa es el valor de uno de los lados del cuadrado. Para calcular el área del cuadrado utilizaremos la siguiente fórmula:
Area del cuadrado= Lado*Lado
Area del cuadrado= Raiz(45)* Raiz(45)=45
Por lo que el área del cuadrado es de 45 cm^2