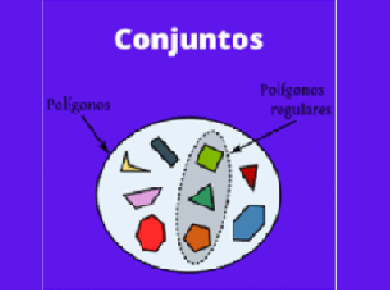
Un conjunto es una cantidad determinada de objetos, estos objetos pueden ser cualquier cosa: números, personas, colores, etc. Ciertos ejemplos son: números naturales y grupo de los colores verde, blanco y rojo.
A continuación se pueden apreciar los siguientes ejercicios de conjuntos:
3 ejercicios divertidos de teoría de conjuntos
La teoría de conjuntos definen a un conjunto matematico como una cantidad de elementos que tienen características parecidas. Existen conjuntos ...
3 ejercicios didácticos de union de conjuntos
Las operaciones de union de conjuntos o intersección entre conjuntos matematicos definen a una cantidad de elementos que tienen características ...
3 ejercicios de operaciones entre conjuntos
Las operaciones entre conjuntos matematicos definen a una cantidad de elementos que tienen características parecidas. Existen conjuntos en números, letras, ...
2 sorprendentes operaciones con conjuntos ejercicios
Comprender la teoría de operaciones con conjuntos ejercicios nos permite utilizar los conjuntos como herramienta para analizar, clasificar y ordenar los ...
¿Qué son las operaciones entre conjuntos?
La Teoría de operaciones entre conjuntos es una teoría matemática, que estudia básicamente a un cierto tipo de objetos llamados conjuntos ...
3 ejercicios de operacion con conjuntos
oLa operacion con conjuntos se basa en la separación de elementos con la misma característica. El concepto de conjunto es ...
3 ejercicios de operaciones con conjuntos
Las operaciones con conjuntos en forma enumerativa son aquellos conjuntos que sus elementos tienen una lista de cada cosa que ...
¿Puedes resolver estos cuatro ejercicios de conjuntos matematicos?
Los conjuntos matematicos se definen a una cantidad de elementos que tienen características parecidas. Existen conjuntos en números, letras, figuras, ...
Ejercicios ¿ Que son conjuntos ?
¿ Que son conjuntos ? Se llama conjunto a toda agrupación de cosas, animales, personas o números bien definidos que ...
3 problemas de conjuntos resueltos
En el presente artículo veremos problemas de conjuntos resueltos. Un conjunto son elementos que están agrupados y que tienen las ...
3 ejercicios divertidos de teoría de conjuntos
La teoría de conjuntos definen a un conjunto matematico como una cantidad de elementos que tienen características parecidas. Existen conjuntos ...
3 ejercicios didácticos de union de conjuntos
Las operaciones de union de conjuntos o intersección entre conjuntos matematicos definen a una cantidad de elementos que tienen características ...
3 ejercicios de operaciones entre conjuntos
Las operaciones entre conjuntos matematicos definen a una cantidad de elementos que tienen características parecidas. Existen conjuntos en números, letras, ...
2 sorprendentes operaciones con conjuntos ejercicios
Comprender la teoría de operaciones con conjuntos ejercicios nos permite utilizar los conjuntos como herramienta para analizar, clasificar y ordenar los ...
¿Qué son las operaciones entre conjuntos?
La Teoría de operaciones entre conjuntos es una teoría matemática, que estudia básicamente a un cierto tipo de objetos llamados conjuntos ...
3 ejercicios de operacion con conjuntos
oLa operacion con conjuntos se basa en la separación de elementos con la misma característica. El concepto de conjunto es ...
3 ejercicios de operaciones con conjuntos
Las operaciones con conjuntos en forma enumerativa son aquellos conjuntos que sus elementos tienen una lista de cada cosa que ...
¿Puedes resolver estos cuatro ejercicios de conjuntos matematicos?
Los conjuntos matematicos se definen a una cantidad de elementos que tienen características parecidas. Existen conjuntos en números, letras, figuras, ...
Ejercicios ¿ Que son conjuntos ?
¿ Que son conjuntos ? Se llama conjunto a toda agrupación de cosas, animales, personas o números bien definidos que ...
3 problemas de conjuntos resueltos
En el presente artículo veremos problemas de conjuntos resueltos. Un conjunto son elementos que están agrupados y que tienen las ...
En general hay diferentes conjuntos, útiles para las matemáticas los más importantes son:
- Conjuntos equivalentes: Los conjuntos equivalentes son esos que tienen la misma cardinalidad, que es el número de recursos que tiene un grupo. En otros términos, mencionamos que 2 (o más) conjuntos son iguales si dichos poseen la misma proporción de recursos.
- Conjuntos finitos: En matemáticas, un grupo finito es un grupo que tiene un número limitado de recursos. La cardinalidad o número de recursos de un grupo limitado es igual a un número natural.
- Conjuntos infinitos: Si un grupo no es finito, entonces es infinito. Ejemplificando, el grupo N = {1, 2, 3, …} este es infinito.
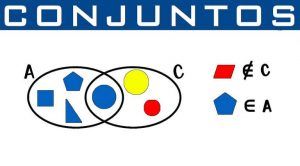
- Conjuntos disjuntos o disyuntivos: En matemáticas, 2 conjuntos son disjuntos o ajenos si no poseen ningún componente en común. Equivalentemente, 2 conjuntos son disjuntos si su intersección es vacía. Ejemplificando, {1, 2, 3} y {a, b, c} son conjuntos disjuntos.
- Conjuntos iguales: Se plantea que 2 conjuntos son iguales si poseen exactamente los mismos recursos. Una forma práctica de implantar si 2 conjuntos son equivalentes es decidir si se tienen dentro el uno al otro. Ejemplificando, para revisar si los conjuntos y de la imagen son equivalentes, debemos comprobar si y además si .
- Conjuntos unitarios: Los números unitarios corresponden a todos los conjuntos de números que se hallan formados por una sola cifra, corresponde a los números que van a partir del 0 al 9. Los números primos son esos números que únicamente son divisibles entre sí mismo y entre el número uno.
La teoría de los conjuntos es lo suficientemente rica como para la construcción objetos de interés en matemáticas: números, funcionalidades, figuras geométricas, etc; debido a los instrumentos de la lógica, posibilita aprender los fundamentos.
En teoría de conjuntos, un número cardinal son números naturales para contar el número de recursos, la cardinalidad, de cualquier grupo, limitado o infinito. El cardinal de un grupo limitado es un número natural ordinario.
Es usual representar los conjuntos en forma gráfica por medio de los Diagramas de Venn . En dichos diagramas el Grupo se representa por medio de una área reducida por una línea. En su interior se colocan los recursos del grupo.
Para comprender fácilmente los conjuntos, se utilizan, en vez de números, recursos como frutas, animales, niños. Lo primero que debemos saber es qué es un conjunto. Tenemos la posibilidad de definirlo como una recolección de objetos, a los que llamamos recursos, que poseen alguna característica común.
3 ejercicios divertidos de teoría de conjuntos
3 ejercicios didácticos de union de conjuntos
3 ejercicios de operaciones entre conjuntos
2 sorprendentes operaciones con conjuntos ejercicios
¿Qué son las operaciones entre conjuntos?
3 ejercicios de operacion con conjuntos
3 ejercicios de operaciones con conjuntos
¿Puedes resolver estos cuatro ejercicios de conjuntos matematicos?
