Los polinomios se parten de acuerdo con la proporción de términos por el cual se encuentre compuesto. Cada polinomio obtiene un nombre particular de acuerdo con el número de términos: binomio, trinomio, y de 4 o más términos lo llamamos polinomios.
¿Que son los polinomios?
Los 3 mejores ejercicios de multiplicación de polinomios
Ejercicios de Polinomios
Ejercicios Suma de polinomios
Resta de polinomios
Multiplicación de polinomios
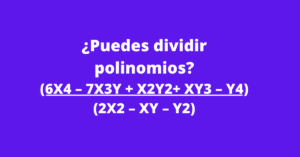
¿Puedes dividir polinomios?
Un polinomio está formado por la suma de vatios monomios.
Un polinomio se plantea que es nulo si todos los monomios que lo conforman poseen coeficiente cero.
Un polinomio está dado en forma limitada si en su expresión no aparecen monomios similares, ni nulos.
Un polinomio es una expresión algebraica de sumas, restas y multiplicaciones ordenadas desarrollada de variables, constantes y exponentes. Cada término es una expresión que tiene uno o bastante más de los 3 recursos de los que permanecen hechos: variables, constantes o exponentes. Ejemplificando: 9, 9x, 9xy son todos términos.
¿Cómo se resuelven los polinomios?
Para poder resolver un polinomio se siguen los siguientes pasos:
Paso 1: Se multiplica cada monomio del primer polinomio por todos los recursos del segundo polinomio.
Paso 2: Se suman los monomios del mismo nivel, obteniendo otro polinomio cuyo nivel es la suma de los grados de los polinomios que se multiplican.
¿Cómo se suman y restan los polinomios?
Sumar o restar polinomios equivale a sumar o restar los monomios (del polinomio) similares. Con una ejemplificación lo observaremos mejor. Si deseamos sumar:
p(x)=x^2−x+1
y q (x)=3x^2+x−2
Agrupamos los monomios similares 2 a 2 y operamos, quedando como resultado lo siguiente:
4x^2−1
¿Cómo se resuelven los polinomios con fracciones?
El resultado se recibe por medio del siguiente proceso: Escribimos los polinomios de tal forma que sus monomios similares queden en columna. Escribimos los polinomios de tal forma que sus monomios similares queden en columna.
Igual que los ejercicios de Suma de Polinomios Enteros, se procede así:
- Para el orden de los polinomios es de grado mayor a menor.
- Se coloca el primer polinomio ordenado de mayor a menor.
- Se copia el segundo polinomio ordenándolo de mayor a menor, colocando los términos semejantes debajo de los del polinomio colocado anteriormente.
- Se suman los términos semejantes de los polinomios, no debemos olvidar los signos.
Ejemplo 1
P(X)= ½ x^2 + 1/3 xy
Q(X)= ½ xy + ¼ y^2
Sumar P(X) + Q(X)
1/2x^2 + 1/3xy
+ 1/2xy + 1/4y^2
1/2x^2 +5/6xy +1/4y^2
Ejemplo 2
P(X)= a^2 + ½ ab
Q(X)= -1/4 ab + ½ b^2
R(X)= -1/4 ab – 1/5 b^2
Sumar P(X) + Q(X) + R(X)
a^2 + 1/2ab
– 1/4ab + 1/2b^2
– 1/4ab – 1/5b^2
a^2 0 + 3/10b^2 = a^2 + 3/10b^2
¿Cuáles son las clases de un polinomio?
Los Tipos de polinomios más utilizados son los siguientes:
- Polinomio nulo.
- Polinomio homogéneo.
- Polinomio heterogéneo.
- Polinomio completo.
- Polinomio inconcluso.
- Polinomio ordenado.
- Polinomios equivalentes.
- Polinomios similares.
