2 ecuaciones con 2 incógnitas conforman un sistema, una vez que lo cual pretendemos de ellas es descubrir su solución común.
a1x+b1y=c1
a2x+b2y=c2
La solución de un sistema es dos números x1,y1, tales que reemplazando x por x1 e y por y1, se satisfacen a la vez las dos ecuaciones.
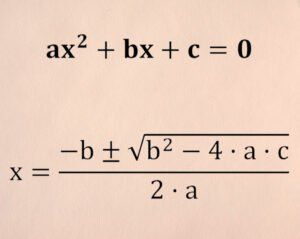
Ecuaciones de segundo grado

Sistemas de Ecuaciones: Procedimientos de resolución
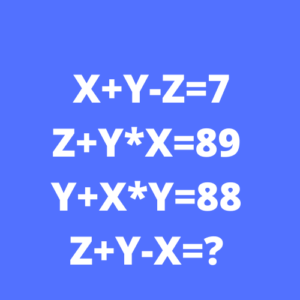
¿Que son las ecuaciones?

3 ejercicios de ecuaciones de primer grado

3 ejercicios de sistemas de ecuaciones lineales con dos incognitas

¿Qué es una ecuacion cuadratica?

¿Qué es un sistema de ecuaciones 2×2?

3 ejercicios para resolver ecuaciones

Sistemas de ecuaciones con dos incognitas

Ejercicios Sistemas de Ecuaciones

¿Cuál es la edad del padre e hijo mediante un sistema de ecuaciones?

¿Cual es el sistema de ecuaciones a plantearse?

¿Qué Métodos existen para resolver sistemas de ecuaciones?

Problemas de sistema de ecuaciones – Aprenda a resolver sistemas de Ecuaciones de forma sencilla
Sistemas iguales
2 sistemas de ecuaciones son iguales una vez que poseen la misma solución.
Criterios de equivalencia
1 Si a los dos miembros de una ecuación de un sistema se les suma o se les resta una misma expresión, el sistema resultante es equivalente.
2 Si multiplicamos o dividimos los dos miembros de las ecuaciones de un sistema por un número diferente de cero, el sistema resultante es equivalente.
3 Si sumamos o restamos a una ecuación de un sistema otra ecuación del mismo sistema, el sistema resultante es igual al dado.
4 Sin en un sistema se suple una ecuación por otra que resulte de sumar ambas ecuaciones del sistema antes multiplicadas o divididas por números no nulos, resulta otro sistema equivalente al primero.
5 Si se cambia el orden de las ecuaciones o incógnitas, resulta un sistema equivalente.
Resolución de sistemas de ecuaciones
Hay diversos procedimientos para solucionar sistemas de ecuaciones, en este artículo mostraremos 3 de los más usados.
Método de sustitución
1 En cualquiera de las ecuaciones se deberá despejar una incógnita.
2 Se reemplaza la expresión de esta incógnita en la otra ecuación, obteniendo una ecuación con una sola incógnita.
3 Se resuelve la ecuación.
4 El costo obtenido se suple en la ecuación en la que se mostraba la incógnita despejada.
5 Ambos valores logrados conforman la solución del sistema.
Método de igualación
1 Se debe tomar en cuenta que la incógnita a despejar en ambas ecuaciones es la misma.
2 Se igualan las expresiones y obtenemos una incógnita en una ecuación.
3 Se resuelve la ecuación.
4 El costo obtenido se suple en cualquier persona de ambas expresiones en las que se mostraba despejada la otra incógnita.
Método de reducción
1 Se preparan ambas ecuaciones, multiplicándolas por los números que convenga.
2 La restamos o sumamos de manera que desaparece una de las incógnitas.
3 Se resuelve la ecuación resultante.
4 El costo obtenido se reemplaza en una de las ecuaciones iniciales y se resuelve.
Tipos de sistemas
Sistema compatible definido
Tiene una sola solución.
Gráficamente la solución es el punto de corte de ambas rectas.
Ejemplo: Encontrar las resoluciones del sistema
4x+5y=1
2x-y=5
Aplicamos el procedimiento de reducción, para lo que multiplicamos por 5 los dos lados de la segunda ecuación y se recibe el sistema equivalente
4x+5y=1
10x-5y=25
Sumamos las dos ecuaciones y resolvemos la ecuación resultante
4x+5y=1
10x-5y=25
14x=26
x=26/14
Sustituimos el costo anterior en la segunda ecuación
2x-y=5
2(26/14)-y=5
26/7-y=5
26/7-y=35/7
y=-9/7
Sistema compatible indeterminado
El sistema tiene infinitas resoluciones.
Ejemplo: Encontrar las resoluciones del sistema
12X-6Y=30
2X-Y=5
Aplicamos el procedimiento de reducción, para lo que multiplicamos por 6 los dos lados de la segunda ecuación y se recibe el sistema equivalente
12X-6Y=30
12X-6Y=30
Las rectas son equivalentes, por lo cual se poseen infinitas resoluciones. De esta forma, hablamos de un sistema compatible indeterminado
Sistema incompatible
No tiene solución
Ejemplo: Encontrar las resoluciones del sistema
12X-6Y=30
2X-Y=1
Aplicamos el procedimiento de reducción, para lo que multiplicamos por 6 los dos lados de la segunda ecuación y se recibe el sistema equivalente
12X-6Y=30
12X-6Y=1
Las rectas no son equivalentes, empero poseen la misma pendiente m=2 por lo cual son paralelas y no existe solución. De esta forma, hablamos de un sistema incompatible.
[orbital_cluster categories=»7″ order=»DESC» postperpage=»44″]

