En esta página, explicamos cómo realizar la resta de polinomios que es la base para operaciones con fracciones algebraicas. Además, encontrarás varios ejemplos y resolverás gradualmente el problema de la restas de polinomios.
¿Cómo se resta un polinomio?
Para realizar la resta de dos polinomios, se deben restar los términos de polinomios similares. En otras palabras, la resta de polinomios implica restar términos (restar los polinomios) con la misma parte literal (misma variable y mismo exponente).
En matemáticas, se pueden utilizar dos métodos diferentes para calcular la resta de polinomios: el método vertical y el método horizontal. La siguiente es una explicación de estos dos procesos, pero le recomendamos que primero aprenda a restar un polinomio verticalmente y luego continúe usando el método horizontal. A continuación, usaremos un ejemplo para aprender a restar dos polinomios verticalmente:
Resta de polinomios vertical
- Utilice dos polinomios para realizar la resta P (X) -Q (X):
P (X) = 9X^4 + 4X^3 + 7X – 6
Q (X) = 5X^4 -6X^3 + 9X^2 -3X +2
Para encontrar cualquier resta de un polinomio, lo primero que debemos hacer es colocar un polinomio debajo del otro polinomio para que los términos similares de los dos polinomios estén alineados en columnas:
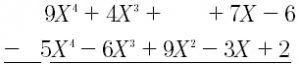
Si el polinomio no tiene un cierto grado de términos, los espacios deben dejarse en blanco. Por ejemplo, el polinomio P (X) = 9X^4 + 4X^3 + 7X – 6 no tiene un polinomio cuadrático, por lo que hay un espacio en blanco en su lugar, esta es la forma de como restar polinomios.
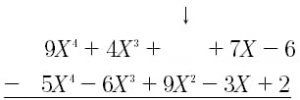
Aunque ahora es posible restar polinomios directamente, es fácil cometer errores si usa este método. Por lo tanto, para realizar una resta de polinomios, es mejor cambiar el signo de todos los términos del polinomio y luego realizar la suma de polinomios del mismo.
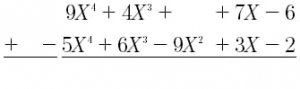
Porque restar un polinomio es igual a sumar sus polinomios opuestos. Una vez que ordenamos todos los términos de mayor a menor, agregamos los coeficientes de cada columna para hacer que la parte del texto sea igual: Por tanto, el resultado de restar los dos polinomios es:
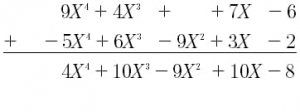
Por lo que el resultado de la resta de los polinomios es la siguiente:
P(X) -Q(X) = 4X^4 + 10X^3 -9X^2 +10X –8
Resta de los polinomios horizontal
Hemos visto cómo restar polinomios verticalmente, pero ahora veremos que hay otra forma de restar polinomios: restar polinomios horizontalmente. Por supuesto, este proceso es más rápido que el proceso anterior, pero es necesario tener una mejor comprensión del concepto de polinomios. Entonces, veamos un método que usa la resta de polinomios. Para que pueda ver la diferencia entre los dos métodos, restaremos el mismo polinomio que en el ejemplo anterior:
La resta computacional son dos polinomios:
P (X) = 9X^4 + 4X^3 + 7X – 6
Q (X) = 5X^4 -6X^3 + 9X^2 -3X +2
Primero, debemos poner dos polinomios en forma de operaciones algebraicas, es decir, uno tras otro: (9X^4 + 4X^3 + 7X – 6 ) – (5X^4 -6X^3 + 9X^2 -3X +2 ). El monomio del primer paréntesis permanece igual, por el contrario, los términos del segundo paréntesis deben cambiar de signo porque van precedidos de un número negativo:
P(X) -Q(X) = 9X^4 + 4X^3 + 7X – 6 –5X^4 +6X^3 – 9X^2 +3X -2
Ahora, agrupamos términos que tienen la misma parte de texto en un grupo, es decir, términos que tienen la misma variable (letra) y el mismo índice. Los términos que no son cercanos no se pueden sumar ni restar. 9X^4 + 4X^3 + 7X – 6 –5X^4 +6X^3 – 9X^2 +3X -2. Por tanto, el polinomio obtenido por resta es: 4X^4 + 10X^3 -9X^2 +10X –8. Como puede ver, logramos los mismos resultados con ambos métodos, por lo que puede utilizar el método más adecuado o que considere que es el más fácil o rápido para su uso.
Ahora que ha visto dos métodos para resolver la resta de polinomios haga click en Resta de polinomios con fracciones o restar fracciones con polinomios
Problemas de la resta de polinomios ejemplos.
Para que practiques, te proporcionamos ejercicios de restas de polinomios. Si tienes alguna duda sobre algún ejercicio, puedes preguntar en los comentarios de la página y te responderemos lo antes posible.
Resta de polinomios: El Polinomio es la suma de varios monomios. Por lo tanto un polinomio, es una expresión algebraica constituida por una o más variables. Con polinomios se realizan operaciones de adición, sustracción, multiplicación y división. En el presente artículo se muestran ejercicios resueltos para la realización de resta de polinomios los cuales se presentan a continuación:
Ejercicio 1: Realizar la resta de los polinomios
A= 2X3-3X2Y + XY2
B = 5X3 – 4X2Y + 2
Para poder realizar la resta de polinomios, el primer paso (inicialmente) se observa los polinomios a restar por grupos quedando de la siguiente manera:
A-B= (2X3-3X2Y + XY2) – (5X3 – 4X2Y + 2)
El segundo paso consiste en multiplicar el signo menos por cada uno de los valores para convertir una resta de polinomios en una suma de polinomios. Quedando de la siguiente manera:
= (2X3-3X2Y + XY2) + (-5X3 + 4X2Y – 2)
Ahora ya podemos trabajar como un ejercicio de suma de polinomios. El tercer paso consiste en la reagrupación por los valores en X que tienen el mismo grado, quedando la suma de polinomios de la siguiente forma:
= (2X3-5X3) + (-3X2Y + 4X2Y) + (XY2) + (- 2)
Como se puede observar se dividieron en cuatro grupos, los valores de X que tienen grado 3, grado 2, grado 1 y grado 0 (es decir, donde no existe X).
El cuarto paso es sumar los valores que tienen el mismo grado, obteniendo los siguientes resultados:
= (-3X3) + (X2Y) + (XY2) + (– 2)
Por lo tanto la suma de polinomios dará como resultado lo siguiente:
= -3X3 +X2Y+XY2 –2
Ejercicio 2: Realizar la resta de polinomios
A= 5X4– 2X2Y2 – XY3 + 3Y4
B = 3X4 +X3Y – X2Y2 + 5Y4
Para poder realizar la resta de polinomios, el primer paso (inicialmente) se observa los polinomios a restar por grupos quedando de la siguiente manera:
A-B= (5X4– 2X2Y2 – XY3 + 3Y4) – (3X4 +X3Y – X2Y2 + 5Y4)
El segundo paso consiste en multiplicar el signo menos por cada uno de los valores para convertir una resta de polinomios en una suma de polinomios. Quedando de la siguiente manera:
= (5X4– 2X2Y2 – XY3 + 3Y4) + (-3X4 -X3Y + X2Y2 – 5Y4)
Ahora ya podemos trabajar como un ejercicio de suma de polinomios. El tercer paso consiste en la reagrupación por los valores en X que tienen el mismo grado, quedando la suma de polinomios de la siguiente forma:
= (5X4– 3X4) + (-X3Y) + (- 2X2Y2 + X2Y2) + (– XY3) + (3Y4– 5Y4)
Como se puede observar se dividieron en cuatro grupos, los valores de X que tienen grado 3, grado 2, grado 1 y grado 0 (es decir, donde no existe X). Vea multiplicación de polinomios.
El cuarto paso es sumar los valores que tienen el mismo grado, obteniendo los siguientes resultados:
= (2X4) + (-X3Y) + (- X2Y2) + (– XY3) + (-2Y4)
Por lo tanto la suma de polinomios dará como resultado lo siguiente:
= 2X4 -X3Y – X2Y2 – XY3 -2Y4

